Log-linear models
Poisson regression
Prof. Maria Tackett
Poisson response variables
The following are examples of scenarios with Poisson response variables:
Are the number of motorcycle deaths in a given year related to a state’s helmet laws?
Does the number of employers conducting on-campus interviews during a year differ for public and private colleges?
Does the daily number of asthma-related visits to an Emergency Room differ depending on air pollution indices?
Has the number of deformed fish in randomly selected Minnesota lakes been affected by changes in trace minerals in the water over the last decade?
Poisson Distribution
If Y follows a Poisson distribution, then
P(Y=y)=exp{−λ}λyy!y=0,1,2,…
Poisson Distribution
If Y follows a Poisson distribution, then
P(Y=y)=exp{−λ}λyy!y=0,1,2,…
Features of the Poisson distribution
- Mean and variance are equal (λ)
- Distribution tends to be skewed right, especially when the mean is small
- If the mean is larger, it can be approximated by a Normal distribution
Simulated Poisson distributions
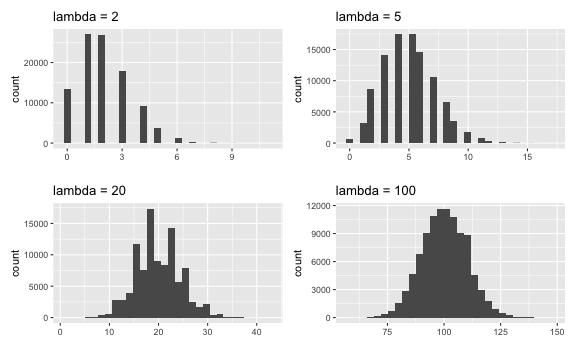
Simulated Poisson distributions
| Mean | Variance | |
|---|---|---|
| lambda=2 | 2.00740 | 2.015245 |
| lambda=5 | 4.99130 | 4.968734 |
| lambda=20 | 19.99546 | 19.836958 |
| lambda=100 | 100.02276 | 100.527647 |
Poisson Regression
- We want λ to be a function of predictor variables x1,…,xp
Poisson Regression
- We want λ to be a function of predictor variables x1,…,xp
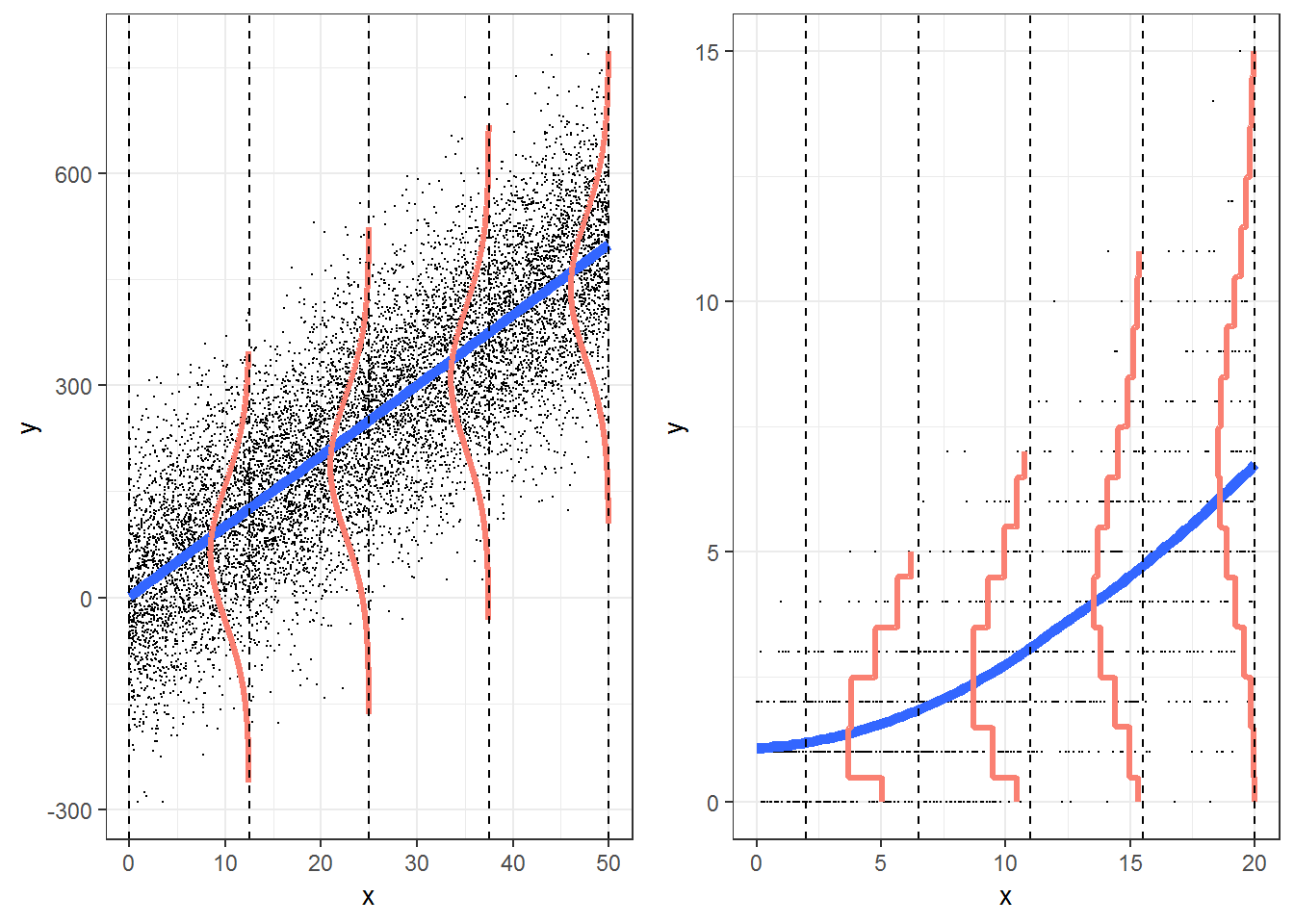
Why is a multiple linear regression model not appropriate?
Poisson Regression
- We want λ to be a function of predictor variables x1,…,xp
Why is a multiple linear regression model not appropriate?
- λ must be greater than or equal to 0 for any combination of predictor variables
- Constant variance assumption will be violated!
Poisson Regression
If the observed values Yi are Poisson, then we can model using a Poisson regression model of the form
log(λi)=β0+β1x1i+β2x2i+⋯+βpxpi
Interpreting Model Coefficients
Slope, βj:
Quantitative Predictor: When xj increases by one unit, the mean of y is expected to multiply by a factor of exp{βj}, (holding all else constant).
Categorical Predictor: The mean of y for category k is expected to be exp{βj} times the mean of y for the baseline category, (holding all else constant).
Interpreting Model Coefficients
Slope, βj:
Quantitative Predictor: When xj increases by one unit, the mean of y is expected to multiply by a factor of exp{βj}, (holding all else constant).
Categorical Predictor: The mean of y for category k is expected to be exp{βj} times the mean of y for the baseline category, (holding all else constant).
- Intercept, β0: When all of the predictors equal 0, the mean of y is expected to be exp{β0}.
Example: Household size in the Philippines
The data come from the 2015 Family Income and Expenditure Survey conducted by the Philippine Statistics Authority.
Goal: We want to use the data to understand the relationship between the age of the head of the household and the number of people in their household.
Variables
age: the age of the head of householdtotal: the number of people in the household other than the head
Exploratory data analysis
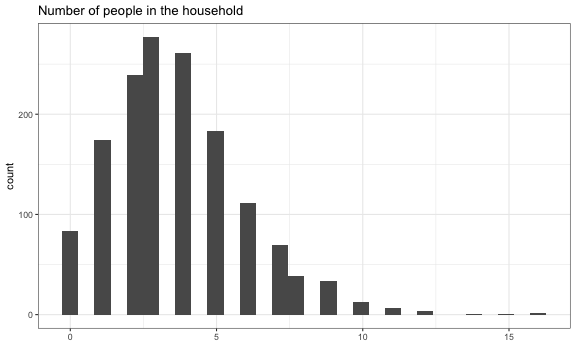
Exploratory data analysis
Let's examine a plot of the log-transformed mean number of people in the household by age
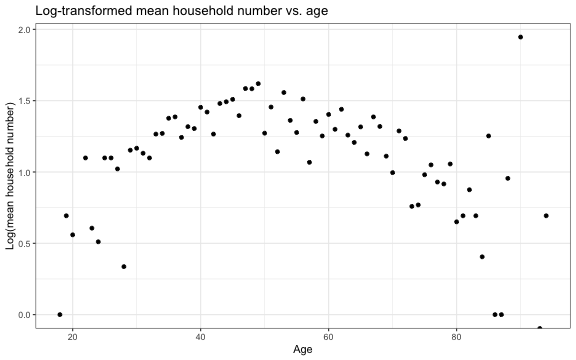
Exploratory data analysis
Let's examine a plot of the log-transformed mean number of people in the household by age
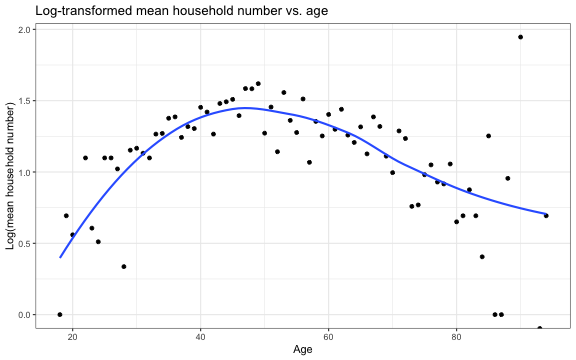
Number in household vs. age
model1 <- glm(total ~ ageCent, data = hh, family = "poisson")tidy(model1, conf.int = T) %>% kable(digits = 3)| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 1.303 | 0.013 | 96.647 | 0 | 1.276 | 1.329 |
| ageCent | -0.005 | 0.001 | -4.832 | 0 | -0.006 | -0.003 |
log(¯total)=1.303−0.0047×ageCent
Interpretations
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 1.303 | 0.013 | 96.647 | 0 | 1.276 | 1.329 |
| ageCent | -0.005 | 0.001 | -4.832 | 0 | -0.006 | -0.003 |
Interpretations
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 1.303 | 0.013 | 96.647 | 0 | 1.276 | 1.329 |
| ageCent | -0.005 | 0.001 | -4.832 | 0 | -0.006 | -0.003 |
For each additional year older the head of the household is, we expect the mean number in the house to multiply by a factor of 0.995 (exp(-0.0047)).
Interpretations
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 1.303 | 0.013 | 96.647 | 0 | 1.276 | 1.329 |
| ageCent | -0.005 | 0.001 | -4.832 | 0 | -0.006 | -0.003 |
For each additional year older the head of the household is, we expect the mean number in the house to multiply by a factor of 0.995 (exp(-0.0047)).
For households with a head of the household who is 52.657 years old, we expect the mean number of people in the household to be 3.68 (exp(1.303)).
Drop-In-Deviance Test
We can use a drop-in-deviance test to compare nested models (similar to logistic regression).
Let's try adding ageCent^2 to the model.
H0:βageCent2=0 vs. Ha:βageCent2≠0
model1 <- glm(total ~ ageCent, data = hh, family = "poisson")model2 <- glm(total ~ ageCent + I(ageCent^2), data = hh, family = "poisson")anova(model1, model2, test = "Chisq")Drop-In-Deviance Test
| Resid. Df | Resid. Dev | Df | Deviance | Pr(>Chi) |
|---|---|---|---|---|
| 1496 | 2330.729 | NA | NA | NA |
| 1495 | 2198.533 | 1 | 132.197 | 0 |
Drop-In-Deviance Test
| Resid. Df | Resid. Dev | Df | Deviance | Pr(>Chi) |
|---|---|---|---|---|
| 1496 | 2330.729 | NA | NA | NA |
| 1495 | 2198.533 | 1 | 132.197 | 0 |
The p-value is small, so we reject H0. We will include ageCent^2 to the model.
Final model
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 1.436 | 0.017 | 82.339 | 0 | 1.402 | 1.470 |
| ageCent | -0.004 | 0.001 | -3.584 | 0 | -0.006 | -0.002 |
| I(ageCent^2) | -0.001 | 0.000 | -10.938 | 0 | -0.001 | -0.001 |
Model Assumptions
Poisson Response: The response follows a Poisson distribution for each level of the predictor.
Independence: The observations are independent of one another.
Mean = variance: The mean value of the response equals the variance of the response for each level of the predictor.
Linearity: log(λ) is a linear function of the predictors.
Poisson response
Let's check the first assumption by looking at the distribution of the response for groups of the predictor.
hh <- hh %>% mutate(age_group = cut(age, breaks = seq(15, 100, 5)))Poisson response
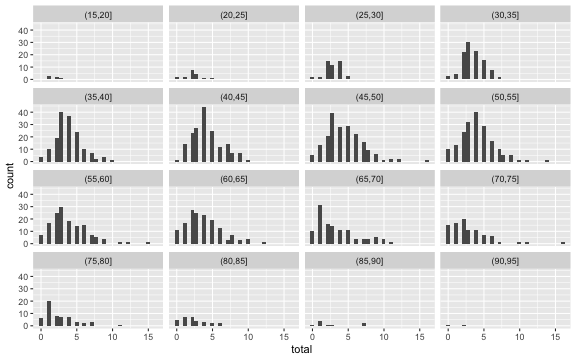
This condition is satisfied based on the overall distribution of the response (from the EDA) and the distribution of the response by age group.
Independence
We don't have much information about how the households were selected for the survey.
If the households were not selected randomly but rather groups of household were selected from different areas with different customs about living arrangements, then the independence assumption would be violated.
Mean = variance
Let's look at the mean and variance for each age group.
## # A tibble: 10 x 4## age_group mean_total var_total n## <fct> <dbl> <dbl> <int>## 1 (15,20] 1.67 0.667 6## 2 (20,25] 2.17 1.56 18## 3 (25,30] 2.92 1.41 49## 4 (30,35] 3.44 2.19 108## 5 (35,40] 3.84 3.57 158## 6 (40,45] 4.23 4.44 175## 7 (45,50] 4.49 6.40 194## 8 (50,55] 4.01 5.25 188## 9 (55,60] 3.81 6.53 145## 10 (60,65] 3.71 6.20 153Mean = variance
## # A tibble: 6 x 4## age_group mean_total var_total n## <fct> <dbl> <dbl> <int>## 1 (65,70] 3.34 8.00 115## 2 (70,75] 2.74 6.75 91## 3 (75,80] 2.53 4.97 57## 4 (80,85] 2.23 3.15 30## 5 (85,90] 2.56 7.03 9## 6 (90,95] 1 2 2Mean = variance
## # A tibble: 6 x 4## age_group mean_total var_total n## <fct> <dbl> <dbl> <int>## 1 (65,70] 3.34 8.00 115## 2 (70,75] 2.74 6.75 91## 3 (75,80] 2.53 4.97 57## 4 (80,85] 2.23 3.15 30## 5 (85,90] 2.56 7.03 9## 6 (90,95] 1 2 2It appears the assumption is violated in some age groups; however, the violations are small enough that we can proceed.
Linearity
The raw residual for the ith observation, yi−ˆλi, is difficult to interpret since the variance is equal to the mean in the Poisson distribution.
Linearity
The raw residual for the ith observation, yi−ˆλi, is difficult to interpret since the variance is equal to the mean in the Poisson distribution.
Instead, we can analyze a standardized residual called the Pearson residual. ri=yi−ˆλi√ˆλi
Linearity
The raw residual for the ith observation, yi−ˆλi, is difficult to interpret since the variance is equal to the mean in the Poisson distribution.
Instead, we can analyze a standardized residual called the Pearson residual. ri=yi−ˆλi√ˆλi
We will examine a plot of the Pearson residuals versus the predicted values to check the linearity assumption.
augment function
hh_aug <- augment(model2, type.predict = "response", type.residuals = "pearson")Linearity condition
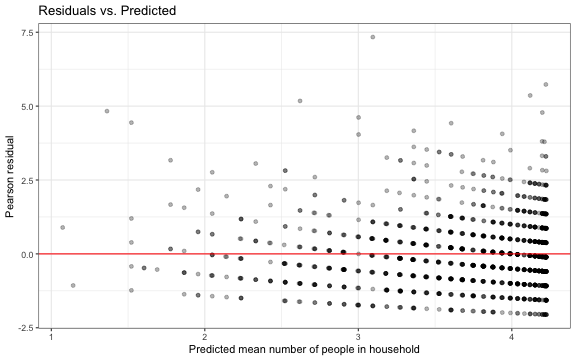
Linearity condition

There is no distinguishable pattern in the residuals, so the linearity assumption is satisfied.