class: center, middle, inverse, title-slide # Logistic regression ## Conditions ### Prof. Maria Tackett --- class: middle, center ## [Click for PDF of slides](20-logistic-conditions.pdf) --- ## Topics - Checking conditions for logistic regression --- ## Risk of coronary heart disease .midi[This dataset is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to examine the relationship between various health characteristics and the risk of having heart disease in the next 10 years.] .midi[.vocab[`high_risk`]: 1 = High risk, 0 = Not high risk] .midi[.vocab[`age`]: Age at exam time (in years)] .midi[.vocab[`totChol`]: Total cholesterol (in mg/dL)] .midi[.vocab[`currentSmoker`]: 0 = nonsmoker; 1 = smoker] --- ## Modeling risk of coronary heart disease |term | estimate| std.error| statistic| p.value| conf.low| conf.high| |:--------------|--------:|---------:|---------:|-------:|--------:|---------:| |(Intercept) | -6.638| 0.372| -17.860| 0.000| -7.374| -5.917| |age | 0.082| 0.006| 14.430| 0.000| 0.071| 0.093| |totChol | 0.002| 0.001| 2.001| 0.045| 0.000| 0.004| |currentSmoker1 | 0.457| 0.092| 4.951| 0.000| 0.277| 0.639| --- ## Conditions for logistic regression 1. .vocab[Linearity]: The log-odds have a linear relationship with the predictors. 2. .vocab[Randomness]: The data were obtained from a random process 3. .vocab[Independence]: The observations are independent from one another. --- ## Empirical logit The .vocab[empirical logit] is the log of the observed odds .eq[ **Empirical logit** `$$\text{logit}(\hat{p}) = \log\Big(\frac{\hat{p}}{1 - \hat{p}}\Big) = \log\Big(\frac{\# \text{Yes}}{\# \text{No}}\Big)$$` ] --- ## Calculating empirical logit (categorical predictor) If the predictor is categorical, we can calculate the empirical logit for each level of the predictor. .midi[ ```r heart %>% count(currentSmoker, high_risk) %>% group_by(currentSmoker) %>% mutate(prop = n/sum(n)) %>% filter(high_risk == "1") %>% mutate(emp_logit = log(prop/(1-prop))) ``` ] --- ## Calculating empirical logit (categorical predictor) If the predictor is categorical, we can calculate the empirical logit for each level of the predictor ``` ## # A tibble: 2 x 5 ## # Groups: currentSmoker [2] ## currentSmoker high_risk n prop emp_logit ## <fct> <fct> <int> <dbl> <dbl> ## 1 0 1 307 0.144 -1.78 ## 2 1 1 328 0.159 -1.67 ``` --- ## Calculating empirical logit (quantitative predictor) 1. Divide the range of the predictor into intervals with approximately equal number of cases. - If you have enough observations, use 5 - 10 intervals. 2. Calculate the mean value of the predictor in each interval. 3. Compute the empirical logit for each interval. -- Then, we can create a plot of the empirical logit versus the mean value of the predictor in each interval. --- ## Empirical logit plot in R (quantitative predictor) .midi[ ```r library(Stat2Data) ``` ```r emplogitplot1(high_risk ~ age, data = heart, ngroups = 10)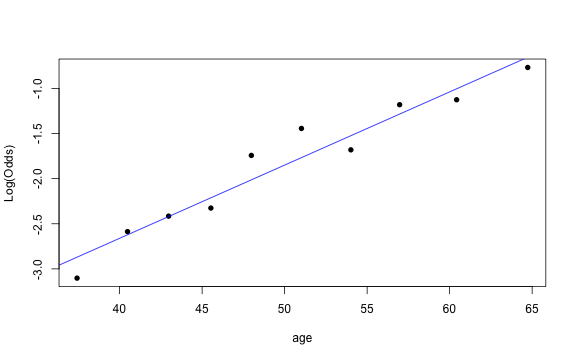 ``` <img src="20-logistic-conditions_files/figure-html/unnamed-chunk-7-1.png" style="display: block; margin: auto;" /> ] --- ## Empirical logit plot in R (interactions) .midi[ ```r library(Stat2Data) ``` ```r emplogitplot2(high_risk ~ age + currentSmoker, data = heart, ngroups = 10, putlegend = "bottomright")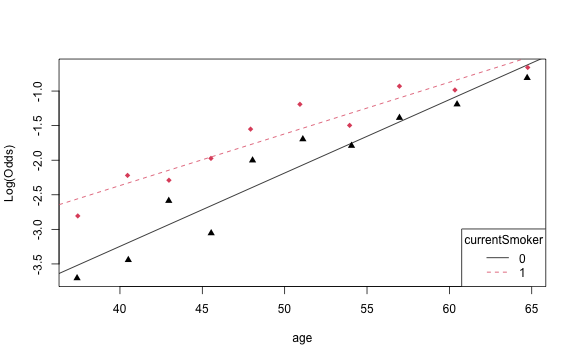 ``` <img src="20-logistic-conditions_files/figure-html/unnamed-chunk-9-1.png" style="display: block; margin: auto;" /> ] --- ## Checking linearity <img src="20-logistic-conditions_files/figure-html/unnamed-chunk-10-1.png" style="display: block; margin: auto;" /> ✅ 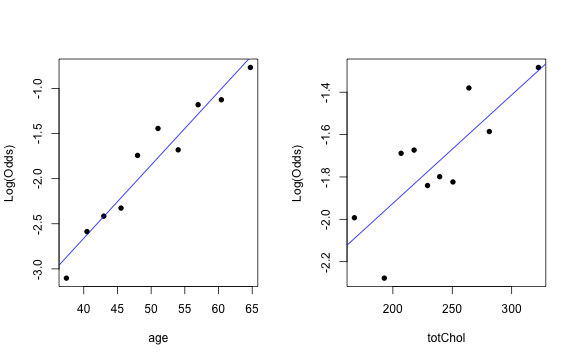The linearity condition is satisfied. There is a linear relationship between the empirical logit and the predictor variables. --- ## Checking randomness We can check the randomness condition based on the context of the data and how the observations were collected. - Was the sample randomly selected? - If the sample was not randomly selected, ask whether there is reason to believe the observations in the sample differ systematically from the population of interest. -- ✅ The randomness condition is satisfied. We do not have reason to believe that the participants in this study differ systematically from adults in the U.S. in regards to health characteristics and risk of heart disease. --- ## Checking independence We can check the independence condition based on the context of the data and how the observations were collected. Independence is most often violated if the data were collected over time or there is a strong spatial relationship between the observations. -- ✅ The independence condition is satisfied. It is reasonable to conclude that the participants' health characteristics are independent of one another. --- class: middle ### What questions do you have about logistic regression? ### [Click here](https://forms.gle/YLD4oKmA9zdLBuB49) to submit your questions.