Logistic regression
Prediction
Prof. Maria Tackett
Topics
Calculating predicted probabilities from the logistic regression model
Using the predicted probabilities to make a "yes/no" decision for a given observation
Assessing model performance using
- Confusion matrix
- ROC curve
Risk of coronary heart disease
This dataset is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to examine the relationship between various health characteristics and the risk of having heart disease in the next 10 years.
high_risk: 1 = High risk, 0 = Not high risk
age: Age at exam time (in years)
totChol: Total cholesterol (in mg/dL)
currentSmoker: 0 = nonsmoker; 1 = smoker
Modeling risk of coronary heart disease
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | -6.638 | 0.372 | -17.860 | 0.000 | -7.374 | -5.917 |
| age | 0.082 | 0.006 | 14.430 | 0.000 | 0.071 | 0.093 |
| totChol | 0.002 | 0.001 | 2.001 | 0.045 | 0.000 | 0.004 |
| currentSmoker1 | 0.457 | 0.092 | 4.951 | 0.000 | 0.277 | 0.639 |
Using the model for prediction
We are often interested in predicting whether a given observation will have a "yes" response
Using the model for prediction
We are often interested in predicting whether a given observation will have a "yes" response
To do so
Using the model for prediction
We are often interested in predicting whether a given observation will have a "yes" response
To do so
- Use the logistic regression model to calculate the predicted log-odds that an observation has a "yes" response.
Using the model for prediction
We are often interested in predicting whether a given observation will have a "yes" response
To do so
Use the logistic regression model to calculate the predicted log-odds that an observation has a "yes" response.
Then, use the log-odds to calculate the predicted probability of a "yes" response.
Using the model for prediction
We are often interested in predicting whether a given observation will have a "yes" response
To do so
Use the logistic regression model to calculate the predicted log-odds that an observation has a "yes" response.
Then, use the log-odds to calculate the predicted probability of a "yes" response.
Then, use the predicted probabilities to classify the observation as having a "yes" or "no" response.
Calculating the predicted probability
Calculating the predicted probability
log(ˆπi1−ˆπi)=ˆβ0+ˆβ1xi
Calculating the predicted probability
log(ˆπi1−ˆπi)=ˆβ0+ˆβ1xi
⇒exp{log(ˆπi1−ˆπi)}=exp{ˆβ0+ˆβ1xi}
Calculating the predicted probability
log(ˆπi1−ˆπi)=ˆβ0+ˆβ1xi
⇒exp{log(ˆπi1−ˆπi)}=exp{ˆβ0+ˆβ1xi} ⇒ˆπi1−ˆπi=exp{ˆβ0+ˆβ1xi}
Calculating the predicted probability
log(ˆπi1−ˆπi)=ˆβ0+ˆβ1xi
⇒exp{log(ˆπi1−ˆπi)}=exp{ˆβ0+ˆβ1xi} ⇒ˆπi1−ˆπi=exp{ˆβ0+ˆβ1xi} ⇒ˆπi=exp{ˆβ0+ˆβ1xi}1+exp{ˆβ0+ˆβ1xi}
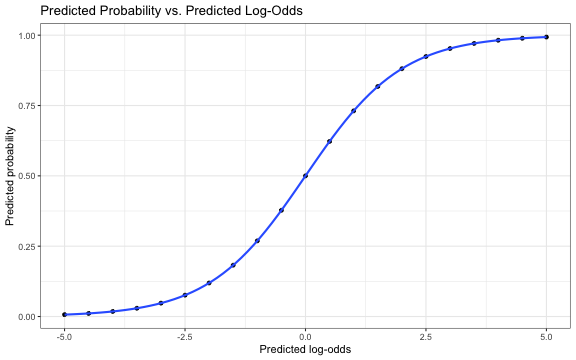
ˆπ vs. ^log-odds
ˆπi=exp(ˆβ0+ˆβ1xi)1+exp(ˆβ0+ˆβ1xi)=exp(ˆlog-odds)1+exp(^log-odds)
Predicted response for a patient
Suppose a patient comes in who is 60 years old, does not currently smoke, and has a total cholesterol of 263 mg/dL.
Predicted response for a patient
Suppose a patient comes in who is 60 years old, does not currently smoke, and has a total cholesterol of 263 mg/dL.
Predicted log-odds that this person is high risk for coronary heart disease in the next 10 years:
^log-odds=−6.638+0.082×60+0.002×263+0.457×0=−1.192
Predicted response for a patient
Suppose a patient comes in who is 60 years old, does not currently smoke, and has a total cholesterol of 263 mg/dL.
Predicted log-odds that this person is high risk for coronary heart disease in the next 10 years:
^log-odds=−6.638+0.082×60+0.002×263+0.457×0=−1.192 The probability this patient is high risk for coronary heart disease in the next 10 years:
^probability=exp{−1.192}1+exp{−1.192}=0.233
Predictions in R
x0 <- data_frame(age = 60, totChol = 263, currentSmoker = factor(0))Predictions in R
x0 <- data_frame(age = 60, totChol = 263, currentSmoker = factor(0))Predicted log-odds
predict(risk_m, x0)## 1 ## -1.214193Predicted probability
predict(risk_m, x0, type = "response")## 1 ## 0.22896Is this patient high risk?
The probability the patient is at risk for coronary heart disease is 0.229.
Is this patient high risk?
The probability the patient is at risk for coronary heart disease is 0.229.
Based on this probability, would you consider this patient as being high risk for getting coronary heart disease in the next 10 years? Why or why not?
Confusion Matrix
- We can use the predicted probability to predict the outcome for a given observation
- In other words, we can classify the observations into two groups: "yes" and "no"
Confusion Matrix
We can use the predicted probability to predict the outcome for a given observation
- In other words, we can classify the observations into two groups: "yes" and "no"
How: Establish a threshold such that y=1 if predicted probability is greater than the threshold (y=0 otherwise)
Confusion Matrix
We can use the predicted probability to predict the outcome for a given observation
- In other words, we can classify the observations into two groups: "yes" and "no"
How: Establish a threshold such that y=1 if predicted probability is greater than the threshold (y=0 otherwise)
To assess the accuracy of our predictions, we can make a table of the observed (actual) response versus the predicted response.
- This table is the confusion matrix
Confusion Matrix
Suppose we use 0.3 as the threshold to classify observations.
If ˆπi>0.3, then risk_predict = "Yes". Otherwise, risk_predict = "No".
| high_risk | risk_predict | n |
|---|---|---|
| 0 | No | 3339 |
| 0 | Yes | 216 |
| 1 | No | 530 |
| 1 | Yes | 105 |
Confusion matrix
| high_risk | risk_predict | n |
|---|---|---|
| 0 | No | 3339 |
| 0 | Yes | 216 |
| 1 | No | 530 |
| 1 | Yes | 105 |
What proportion of observations were misclassified? This is called the misclassification rate.
Confusion matrix: 2 X 2 table
In practice, you often see the confusion matrix presented as a 2 × 2 table as shown below:
| high_risk | No | Yes |
|---|---|---|
| 0 | 3339 | 216 |
| 1 | 530 | 105 |
What is the disadvantage of relying on a single confusion matrix to assess the accuracy of the model?
Receiver Operating Characteristic (ROC) curve
Sensitivity & Specificity
- Sensitivity: Proportion of observations with y=1 that have predicted probability above a specified threshold
- Called true positive rate (y-axis)
Sensitivity & Specificity
Sensitivity: Proportion of observations with y=1 that have predicted probability above a specified threshold
- Called true positive rate (y-axis)
Specificity: Proportion of observations with y=0 that have predicted probability below a specified threshold
- (1 - specificity) called false positive rate (x-axis)
Sensitivity & Specificity
Sensitivity: Proportion of observations with y=1 that have predicted probability above a specified threshold
- Called true positive rate (y-axis)
Specificity: Proportion of observations with y=0 that have predicted probability below a specified threshold
- (1 - specificity) called false positive rate (x-axis)
What we want:
⬆️ High sensitivity
⬇️ Low values of 1-specificity
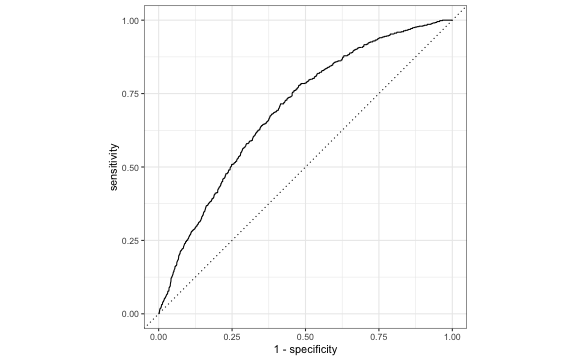
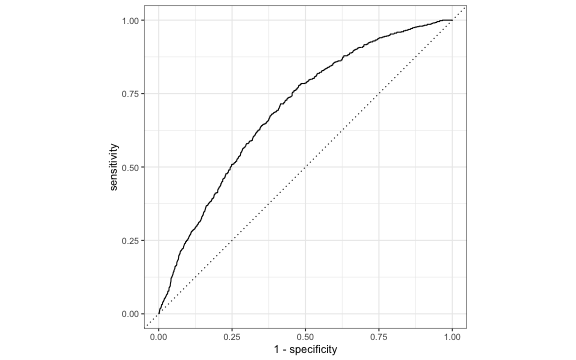
ROC curve in R
library(yardstick)# Need to put 1 as the first levelrisk_m_aug <- risk_m_aug %>% mutate(high_risk = fct_relevel(high_risk, c("1", "0")))# calculate sensitivity and specificity at each thresholdroc_curve_data <- risk_m_aug %>% roc_curve(high_risk, .fitted) # plot roc curveautoplot(roc_curve_data)ROC curve
Area under curve (AUC)
We can use the area under the curve (AUC) as one way to assess how well the logistic model fits the data
- AUC=0.5 very bad fit (no better than a coin flip)
- AUC close to 1: good fit
risk_m_aug %>% roc_auc(high_risk, .fitted) %>% pull(.estimate)## [1] 0.6955Which threshold would you choose?
A doctor plans to use the results from your model to help select patients for a new heart disease prevention program. She asks you which threshold would be best to select patients for this program. Based on the ROC curve from the previous slide, which threshold would you recommend to the doctor? Why?
Recap
Calculating predicted probabilities from the logistic regression model
Using the predicted probabilities to make a "yes/no" decision for a given observation
Assessing model performance using
- Confusion matrix
- ROC curve