+ - 0:00:00
Notes for current slide
Notes for next slide

Multiple linear regression

Inference

Prof. Maria Tackett

1

Click here for PDF of slides

2

Topics

  • Conduct a hypothesis test for βj

  • Calculate a confidence interval for βj

  • Quick overview of math details for MLR

3

House prices in Levittown

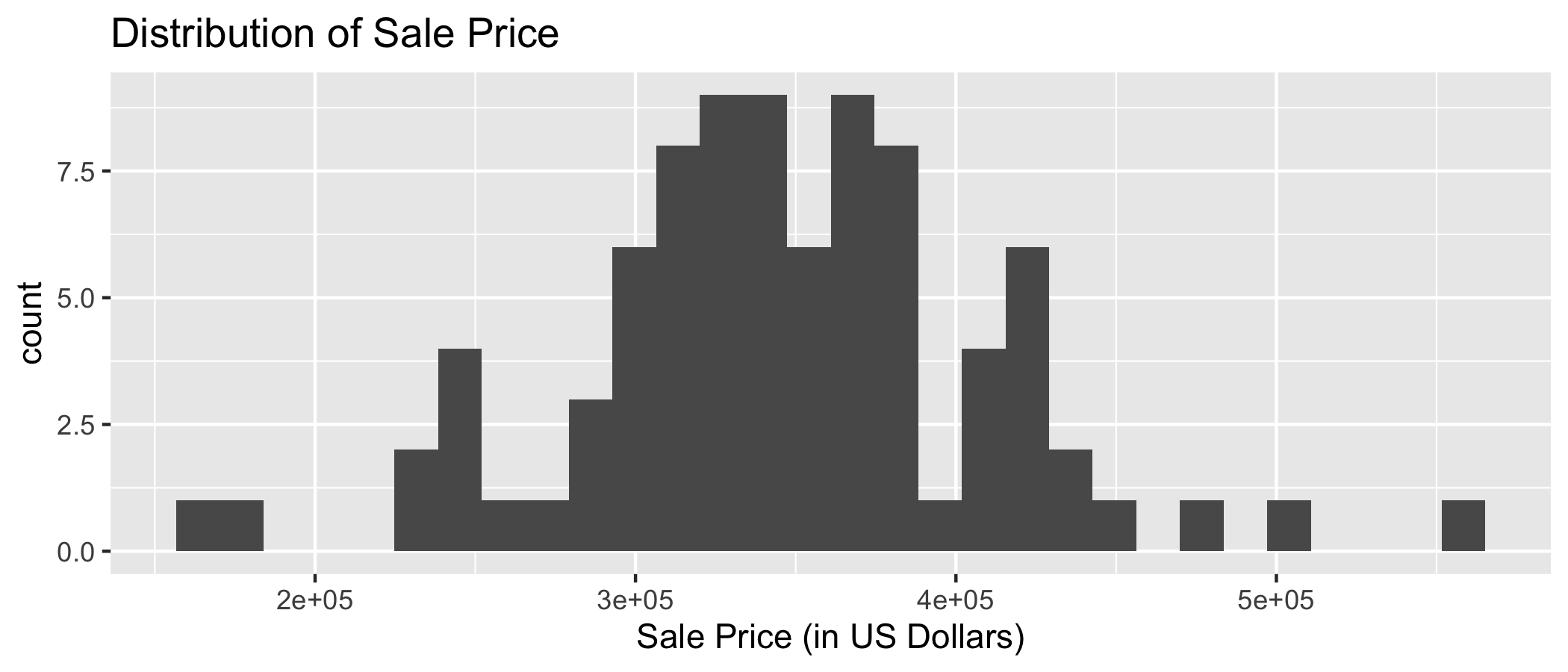
The data set contains the sales price and characteristics of 85 homes in Levittown, NY that sold between June 2010 and May 2011.

We would like to use the characteristics of a house to understand variability in the sales price.

4

Variables

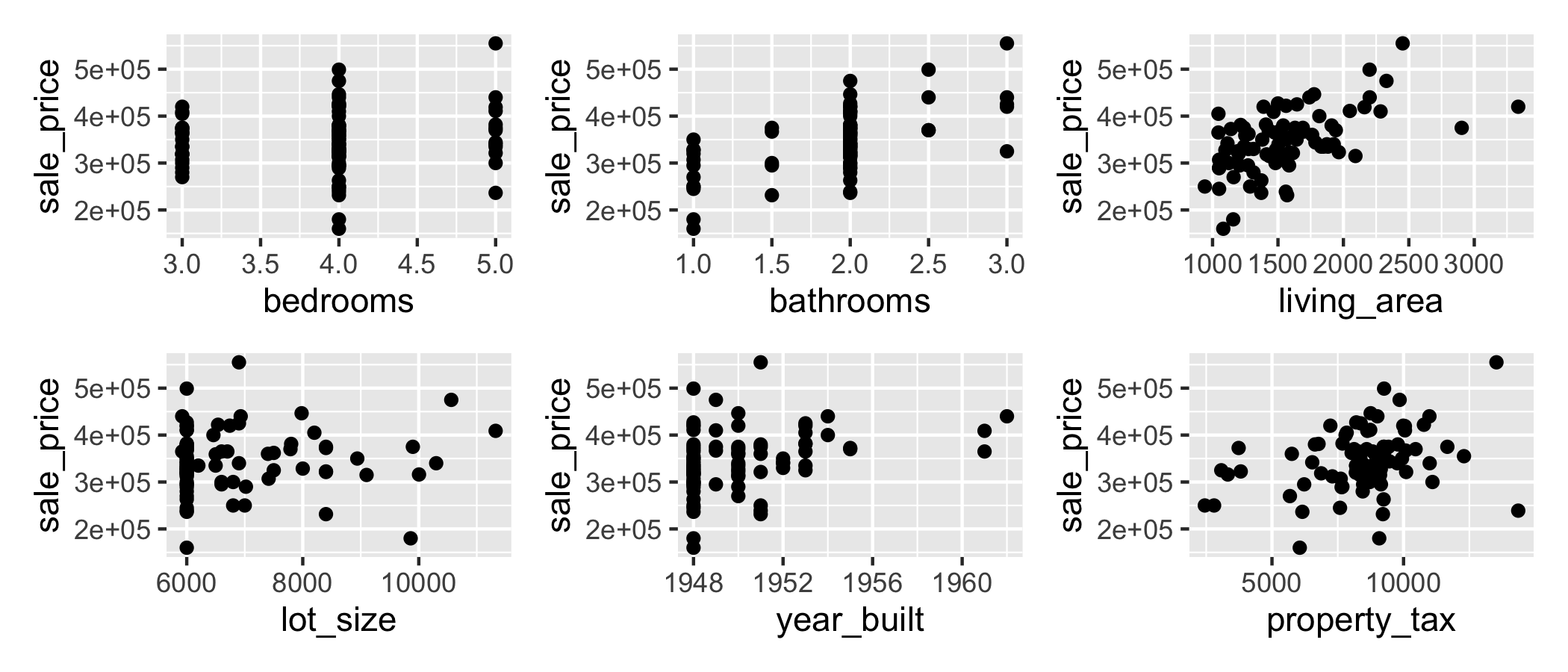
Predictors

  • bedrooms: Number of bedrooms
  • bathrooms: Number of bathrooms
  • living_area: Total living area of the house (in square feet)
  • lot_size: Total area of the lot (in square feet)
  • year_built: Year the house was built
  • property_tax: Annual property taxes (in U.S. dollars)

Response

  • sale_price: Sales price (in U.S. dollars)
5

EDA: Response variable

6

EDA: Response vs. Predictors

7

Home price model

term estimate std.error statistic p.value
(Intercept) -7148818.957 3820093.694 -1.871 0.065
bedrooms -12291.011 9346.727 -1.315 0.192
bathrooms 51699.236 13094.170 3.948 0.000
living_area 65.903 15.979 4.124 0.000
lot_size -0.897 4.194 -0.214 0.831
year_built 3760.898 1962.504 1.916 0.059
property_tax 1.476 2.832 0.521 0.604
8

Hypothesis test for βj

9

Outline of a hypothesis test

10

Outline of a hypothesis test

1️⃣ State the hypotheses.

10

Outline of a hypothesis test

1️⃣ State the hypotheses.


2️⃣ Calculate the test statistic.

10

Outline of a hypothesis test

1️⃣ State the hypotheses.


2️⃣ Calculate the test statistic.


3️⃣ Calculate the p-value.

10

Outline of a hypothesis test

1️⃣ State the hypotheses.


2️⃣ Calculate the test statistic.


3️⃣ Calculate the p-value.


4️⃣ State the conclusion.

10

1️⃣ State the hypotheses

term estimate std.error statistic p.value
(Intercept) -7148818.957 3820093.694 -1.871 0.065
bedrooms -12291.011 9346.727 -1.315 0.192
bathrooms 51699.236 13094.170 3.948 0.000
living_area 65.903 15.979 4.124 0.000
lot_size -0.897 4.194 -0.214 0.831
year_built 3760.898 1962.504 1.916 0.059
property_tax 1.476 2.832 0.521 0.604

H0:βliving_area=0Ha:βliving_area≠0

11

2️⃣ Calculate the test statistic

term estimate std.error statistic p.value
(Intercept) -7148818.957 3820093.694 -1.871 0.065
bedrooms -12291.011 9346.727 -1.315 0.192
bathrooms 51699.236 13094.170 3.948 0.000
living_area 65.903 15.979 4.124 0.000
lot_size -0.897 4.194 -0.214 0.831
year_built 3760.898 1962.504 1.916 0.059
property_tax 1.476 2.832 0.521 0.604

t=65.903−015.979=4.124

12

2️⃣ Calculate the test statistic

The estimated slope, 65.903, is 4.124 standard errors above the hypothesized mean, 0.

13

3️⃣ Calculate the p-value

term estimate std.error statistic p.value
(Intercept) -7148818.957 3820093.694 -1.871 0.065
bedrooms -12291.011 9346.727 -1.315 0.192
bathrooms 51699.236 13094.170 3.948 0.000
living_area 65.903 15.979 4.124 0.000
lot_size -0.897 4.194 -0.214 0.831
year_built 3760.898 1962.504 1.916 0.059
property_tax 1.476 2.832 0.521 0.604

P-value=P(|t|≥|4.124|)=0.00009

14

3️⃣ Calculate the p-value

The p-value is calculated using a t distribution with n−p−1 degrees of freedom, where p is the number of coefficients in the model.

15

3️⃣ Calculate the p-value

The p-value is calculated using a t distribution with n−p−1 degrees of freedom, where p is the number of coefficients in the model.

In this example, the p-value is calculated using a t distribution with 85−6−1=78 degrees of freedom.

15

3️⃣ Calculate the p-value

The p-value is calculated using a t distribution with n−p−1 degrees of freedom, where p is the number of coefficients in the model.

In this example, the p-value is calculated using a t distribution with 85−6−1=78 degrees of freedom.

Given βliving_area=0 the probability of observing a coefficient at least as extreme as the one we've observed, 65.903, is 0.00009.

15

4️⃣ State the conclusion

term estimate std.error statistic p.value
(Intercept) -7148818.957 3820093.694 -1.871 0.065
bedrooms -12291.011 9346.727 -1.315 0.192
bathrooms 51699.236 13094.170 3.948 0.000
living_area 65.903 15.979 4.124 0.000
lot_size -0.897 4.194 -0.214 0.831
year_built 3760.898 1962.504 1.916 0.059
property_tax 1.476 2.832 0.521 0.604

The p-value is very small, so we reject H0. The data provide sufficient evidence that the living area is a helpful predictor in the model explaining some of the variability in price.

16

Confidence interval for βj

17

Confidence Interval for βj

The C confidence interval for βj ˆβj±t∗SE(ˆβj)

where t∗ follows a t distribution with n−p−1 degrees of freedom

General Interpretation: We are C confident that the interval LB to UB contains the population coefficient of xj. Therefore, for every one unit increase in xj, we expect y to change by LB to UB units, holding all else constant.

18

Confidence interval for living_area

term estimate std.error statistic p.value conf.low conf.high
(Intercept) -7148818.957 3820093.694 -1.871 0.065 -14754041.291 456403.376
bedrooms -12291.011 9346.727 -1.315 0.192 -30898.915 6316.893
bathrooms 51699.236 13094.170 3.948 0.000 25630.746 77767.726
living_area 65.903 15.979 4.124 0.000 34.091 97.715
lot_size -0.897 4.194 -0.214 0.831 -9.247 7.453
year_built 3760.898 1962.504 1.916 0.059 -146.148 7667.944
property_tax 1.476 2.832 0.521 0.604 -4.163 7.115

We are 95% confident that for every one additional square foot in living area, we expect the price to increase by $34.09 to $97.71, holding all other characteristics constant.

19

🛑 Caution: Large sample sizes

If the sample size is large enough, the test will likely result in rejecting H0:βj=0 even xj has a very small effect on y

  • Consider the practical significance of the result not just the statistical significance

  • Use the confidence interval to draw conclusions instead of relying only p-values

20

🛑 Caution: Small sample sizes

If the sample size is small, there may not be enough evidence to reject H0:βj=0

  • When you fail to reject the null hypothesis, DON'T immediately conclude that the variable has no association with the response.

  • There may be a linear association that is just not strong enough to detect given your data, or there may be a non-linear association.

21

Math details

22

Regression Model

The multiple linear regression model assumes

Y|X1,X2,…,Xp∼N(β0+β1X1+β2X2+⋯+βpXp,σ2ϵ)

23

Regression Model

The multiple linear regression model assumes

Y|X1,X2,…,Xp∼N(β0+β1X1+β2X2+⋯+βpXp,σ2ϵ)

For a given observation (xi1,xi2,…,xip,yi), we can rewrite the previous statement as

yi=β0+β1xi1+β2xi2+⋯+βpxip+ϵiϵi∼N(0,σ2)

23

Estimating σ2ϵ

For a given observation (xi1,xi2,…,xip,yi) the residual is

ei=yi−(ˆβ0+ˆβ1xi1+ˆβ2xi2+⋯+ˆβpxip)

24

Estimating σ2ϵ

For a given observation (xi1,xi2,…,xip,yi) the residual is

ei=yi−(ˆβ0+ˆβ1xi1+ˆβ2xi2+⋯+ˆβpxip)

The estimated value of the regression variance , σ2ϵ, is

ˆσ2ϵ=∑ni=1e2in−p−1

24

Estimating Coefficients

One way to estimate the coefficients is by taking partial derivatives of the formula

n∑i=1e2i=n∑i=1[yi−(ˆβ0+ˆβ1xi1+ˆβ2xi2+⋯+ˆβpxip)]2

25

Estimating Coefficients

One way to estimate the coefficients is by taking partial derivatives of the formula

n∑i=1e2i=n∑i=1[yi−(ˆβ0+ˆβ1xi1+ˆβ2xi2+⋯+ˆβpxip)]2

This produces messy formulas, so instead we can use matrix notation for multiple linear regression and estimate the coefficients using rules from linear algebra. For more details, see A Matrix Formulation of the Multiple Regression Model.

25

Recap

  • Conduct a hypothesis test for βj

  • Calculate a confidence interval for βj

  • Quick overview of math details for MLR

26

Click here for PDF of slides

2
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow