Simple Linear Regression
Partioning variability
Prof. Maria Tackett
Topics
Topics
- Use analysis of variance to partition variability in the response variable
Topics
Use analysis of variance to partition variability in the response variable
Define and calculate R2
Topics
Use analysis of variance to partition variability in the response variable
Define and calculate R2
Use ANOVA to test the hypothesis
H0:β1=0 vs Ha:β1≠0
Topics
Use analysis of variance to partition variability in the response variable
Define and calculate R2
Use ANOVA to test the hypothesis
H0:β1=0 vs Ha:β1≠0
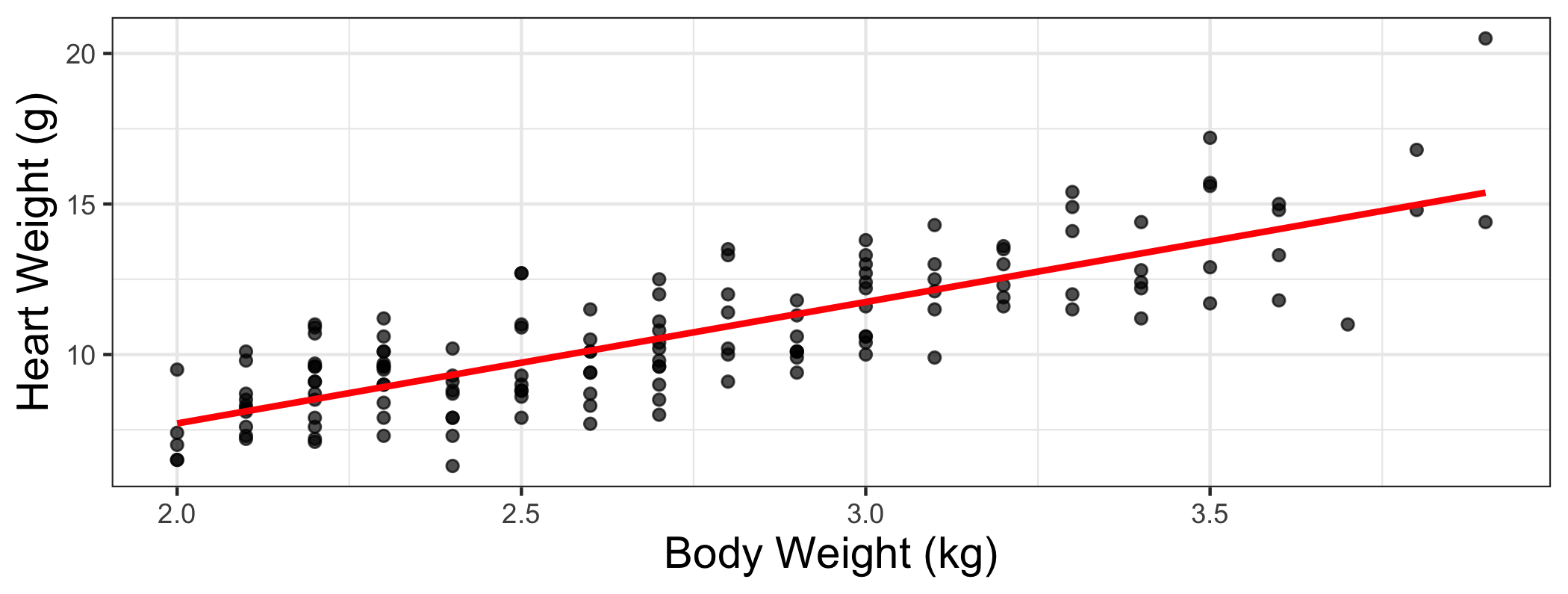
Cats data
The data set contains the heart weight (Hwt) and body weight (Bwt) for 144 domestic cats.
Distribution of response
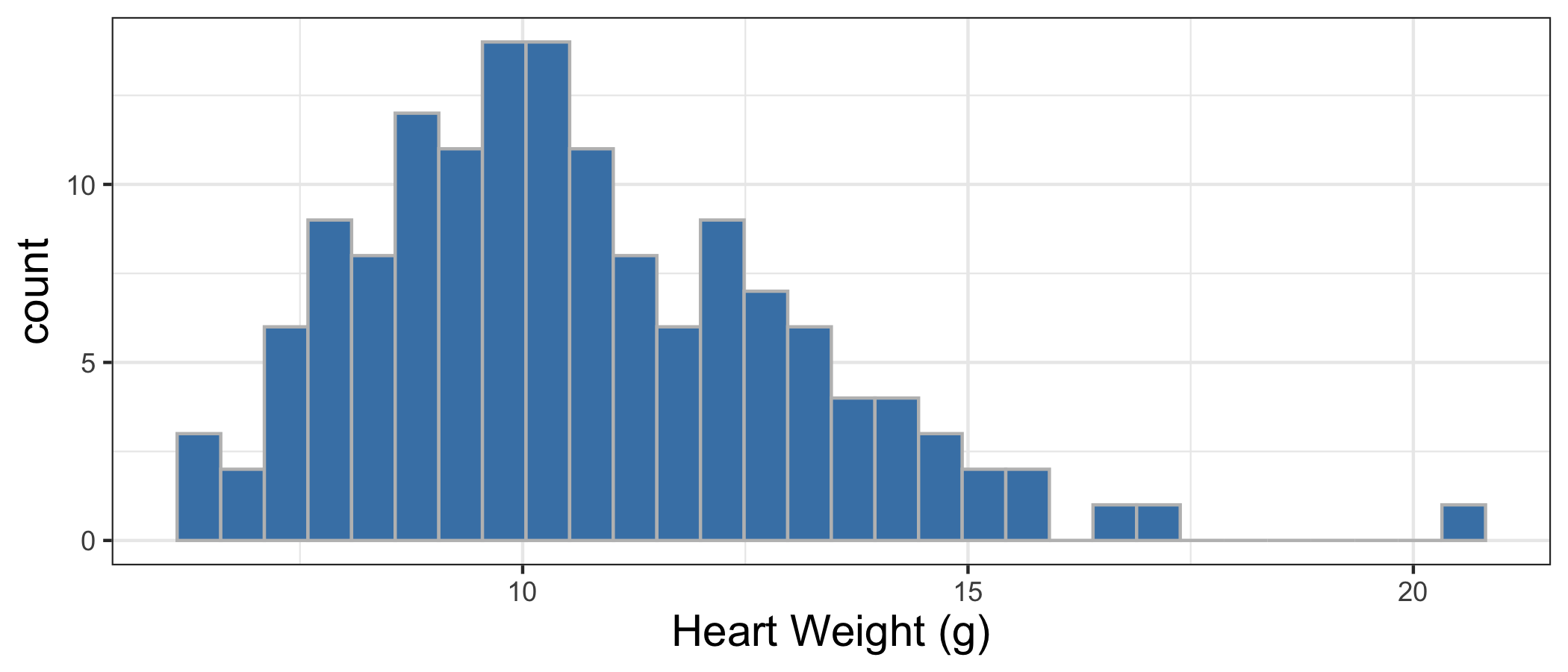
| Mean | Std. Dev. | IQR |
|---|---|---|
| 10.631 | 2.435 | 3.175 |
The model
^Hwt=−0.357+4.034×Bwt
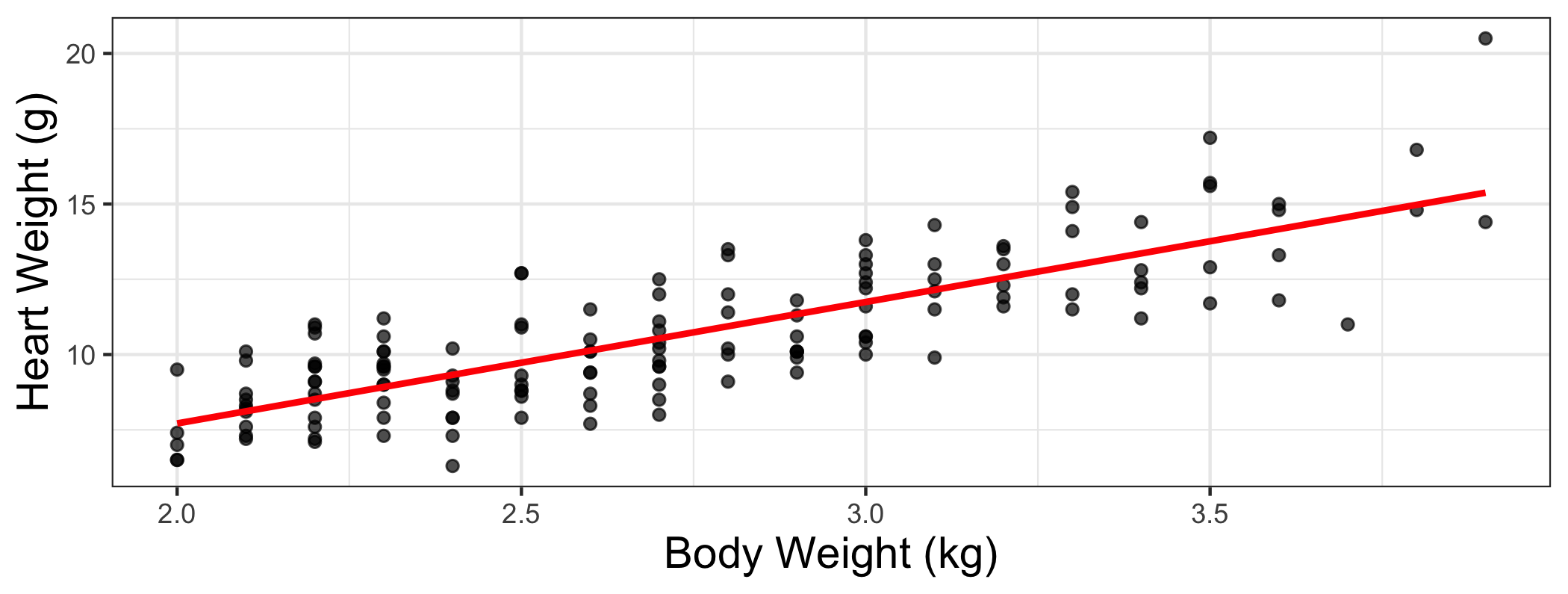
How much of the variation in cats' heart weights can be explained by knowing their body weights?
ANOVA
We will use Analysis of Variance (ANOVA) to partition the variation in the response variable Y.

Response variable, Y
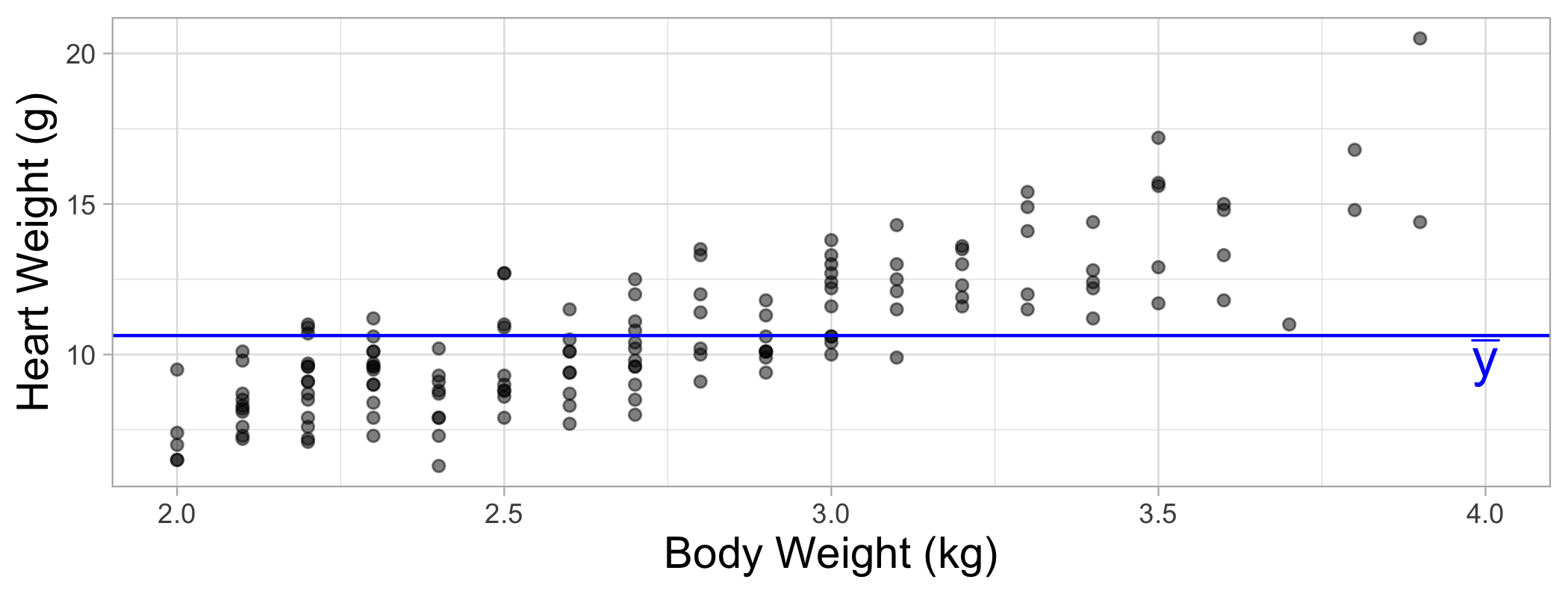
Total variation
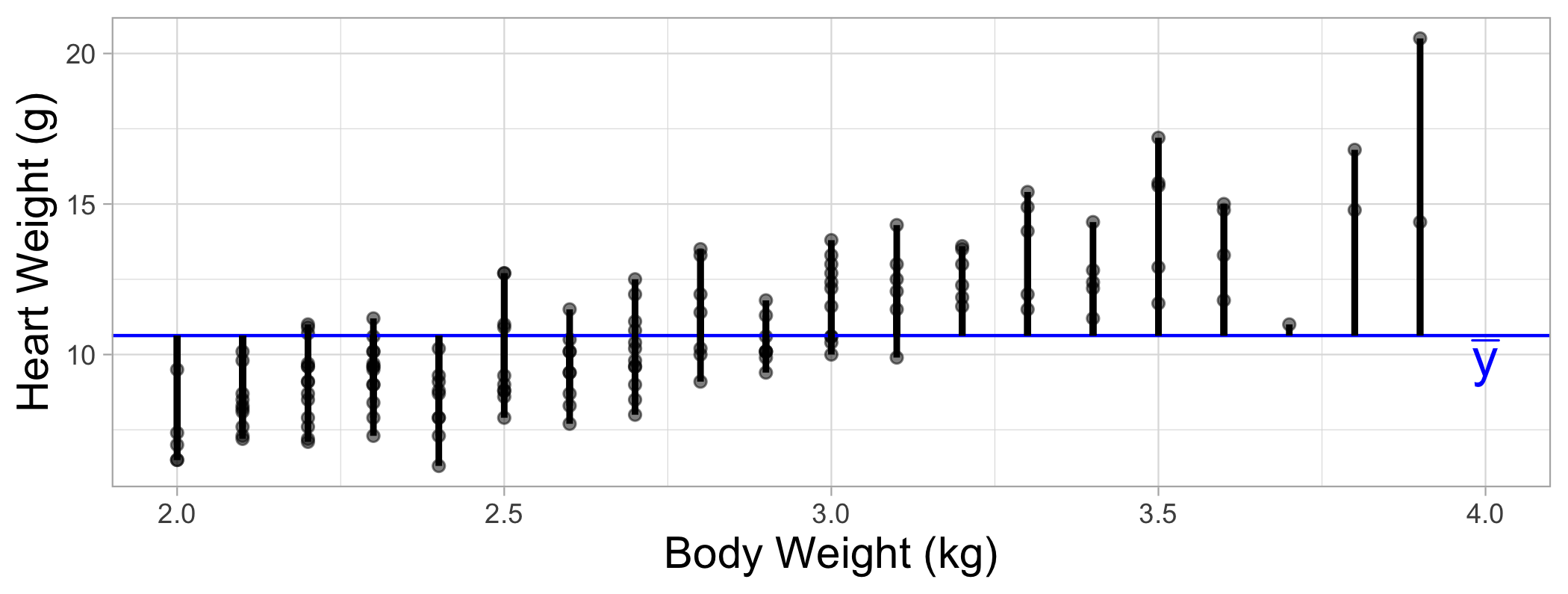
SSTotal=n∑i=1(yi−ˉy)2=(n−1)s2y
Explained variation (Model)
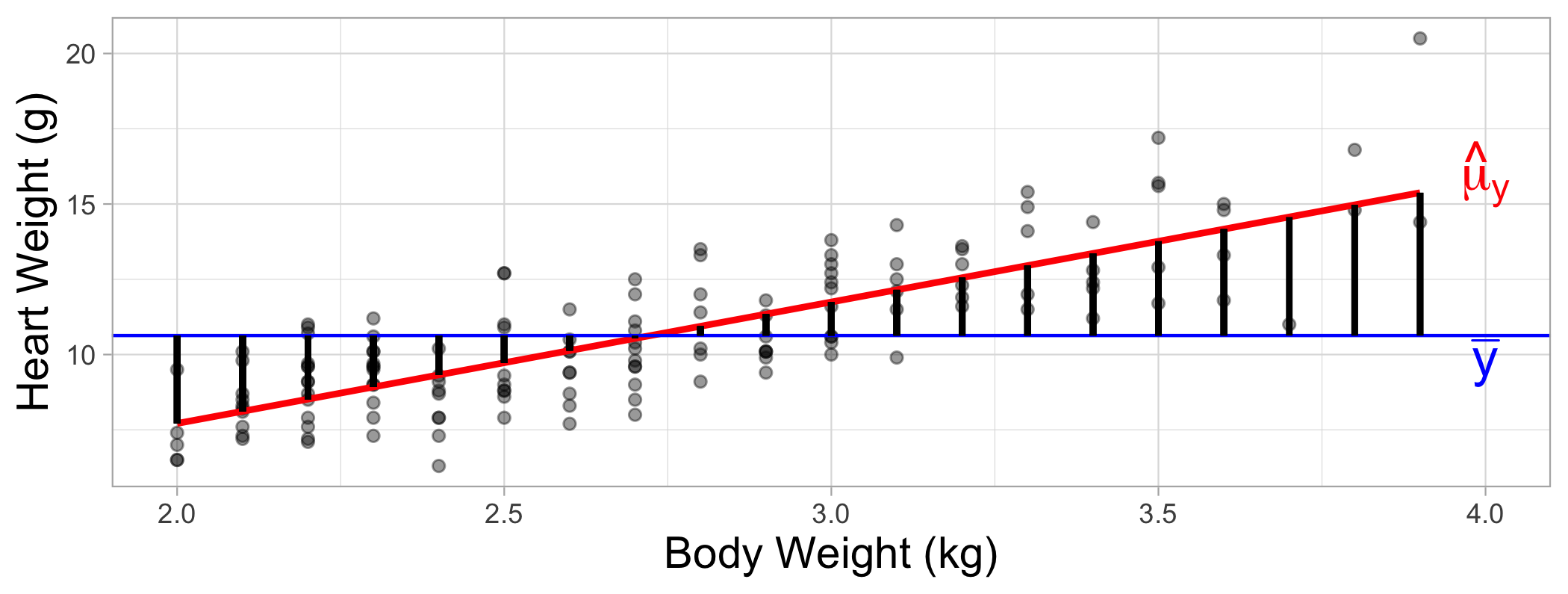
SSModel=n∑i=1(ˆyi−ˉy)2
Unexplained variation (Residuals)
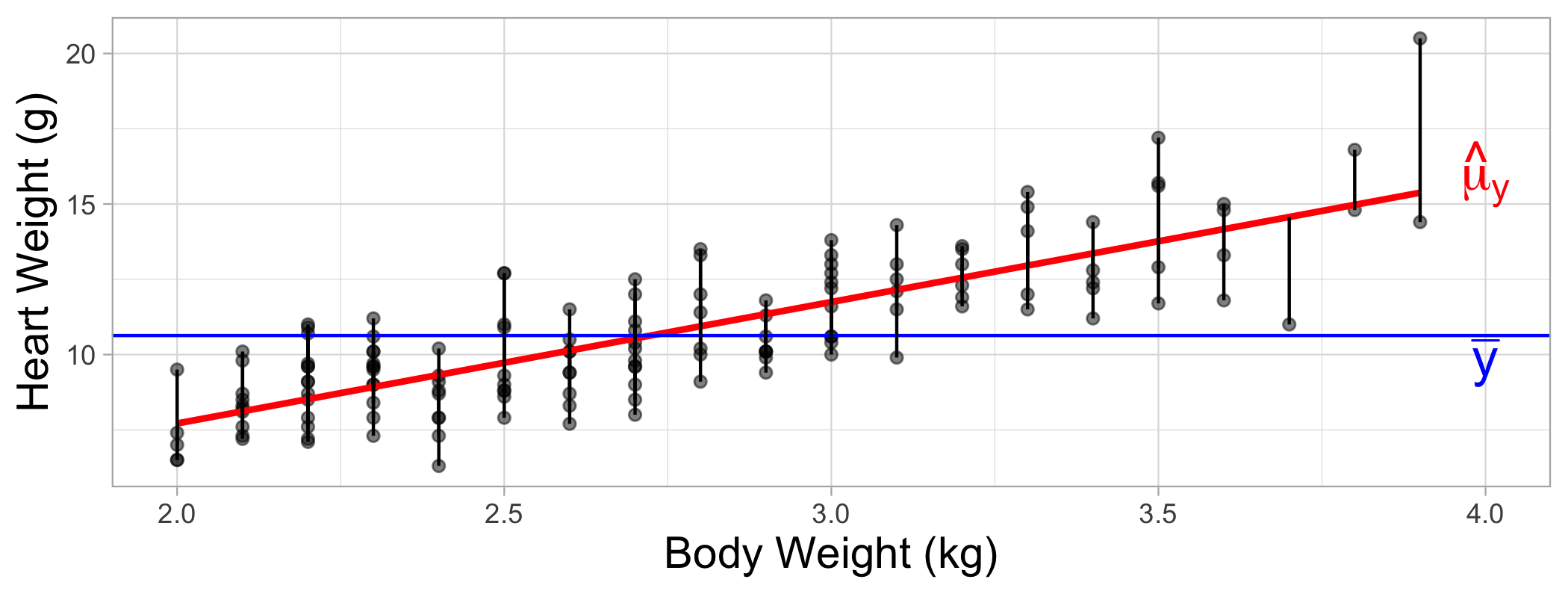
SSError=n∑i=1(yi−ˆyi)2
n∑i=1(yi−ˉy)2=n∑i=1(ˆyi−ˉy)2+n∑i=1(yi−ˆyi)2
n∑i=1(yi−ˉy)2=n∑i=1(ˆyi−ˉy)2+n∑i=1(yi−ˆyi)2
n∑i=1(yi−ˉy)2=n∑i=1(ˆyi−ˉy)2+n∑i=1(yi−ˆyi)2
n∑i=1(yi−ˉy)2=n∑i=1(ˆyi−ˉy)2+n∑i=1(yi−ˆyi)2
R2
The coefficient of determination, R2, is the proportion of variation in the response, Y, that is explained by the regression model
R2
The coefficient of determination, R2, is the proportion of variation in the response, Y, that is explained by the regression model
R2=SSModelSSTotal=1−SSErrorSSTotal
R2 for our model
SSModel=548.092
SSError=299.533
SSTotal=847.625
R2 for our model
SSModel=548.092
SSError=299.533
SSTotal=847.625
R2=548.092847.625=0.647
R2 for our model
SSModel=548.092
SSError=299.533
SSTotal=847.625
R2=548.092847.625=0.647
About 64.7% of the variation in the heart weight of cats can be explained by variation in body weight.
ANOVA table
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA table
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA table
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
Sum of squares
SSTotal=847.625=548.092+299.533
SSModel=548.092
SSError=299.533
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
H0:β1=0Ha:β1≠0
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
Degrees of freedom
dfTotal=144−1=143
dfModel=1
dfError=143−1=142
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
Mean squares
MSModel=548.0921=548.092
MSError=299.533142=2.109
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA Test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
F test statistic: ratio of explained to unexplained variability
F=MSModelMSError=548.0922.109=259.835
F distribution
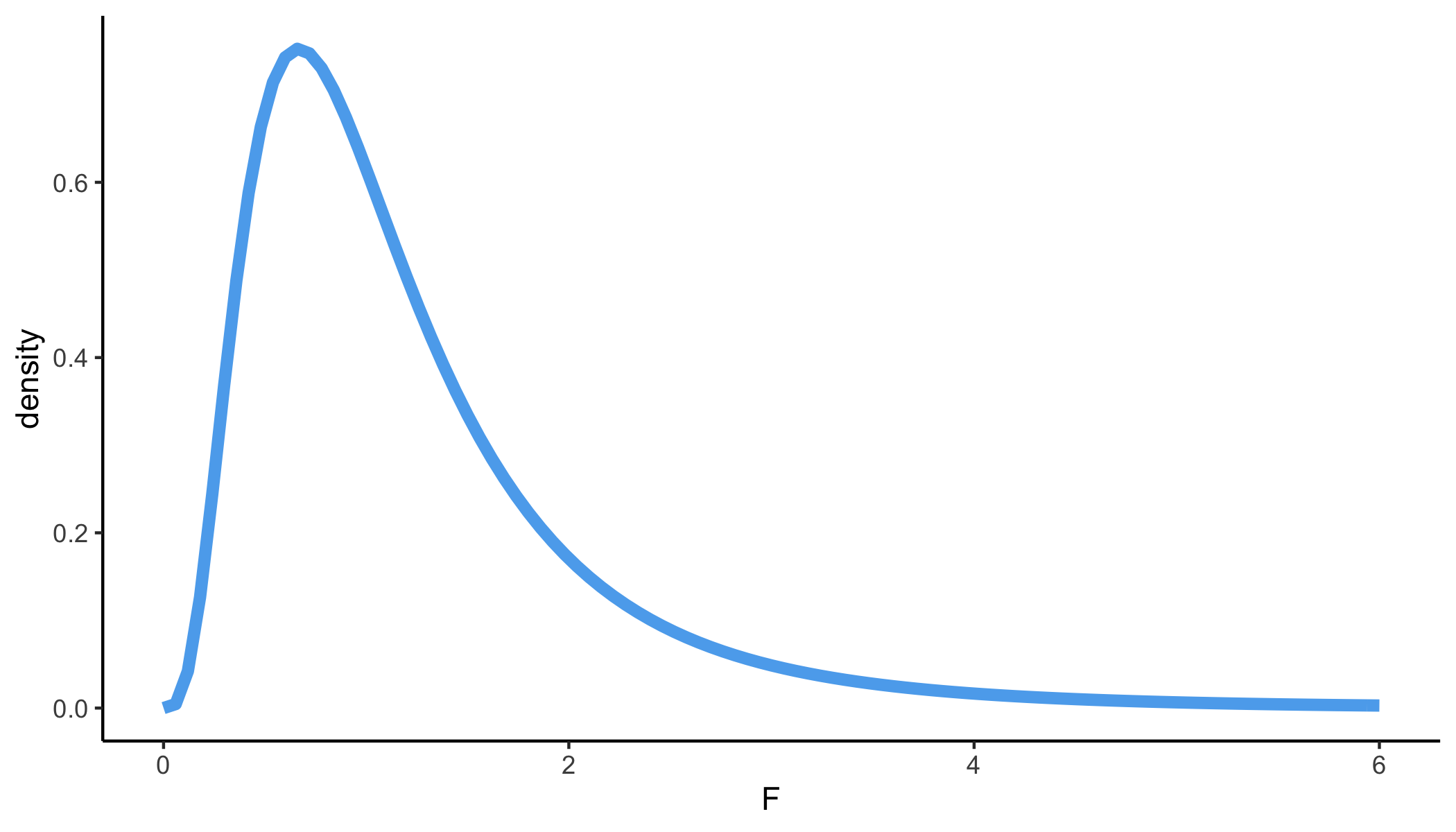
ANOVA test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
ANOVA test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
P-value: Probability of observing a test statistic at least as extreme as F Stat given the population slope β1 is 0
ANOVA test
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
P-value: Probability of observing a test statistic at least as extreme as F Stat given the population slope β1 is 0
The p-value is calculated using an F distribution with 1 and n−2 degrees of freedom
Calculating p-value
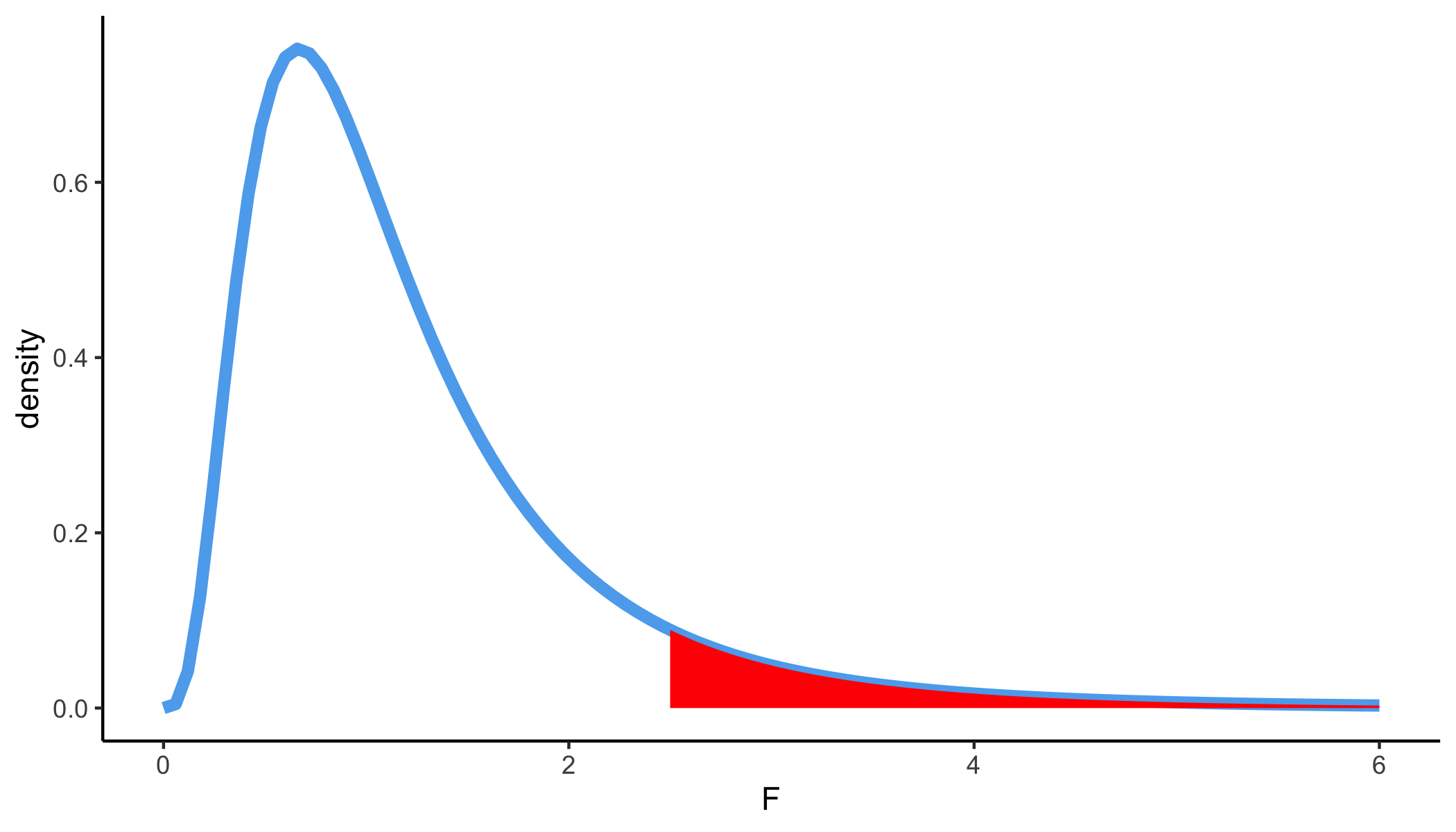
ANOVA
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
The p-value is very small (≈0), so we reject H0.
ANOVA
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
The p-value is very small (≈0), so we reject H0.
The data provide strong evidence that population slope, β1, is different from 0.
ANOVA
| Source | Df | Sum Sq | Mean Sq | F Stat | Pr(> F) |
|---|---|---|---|---|---|
| Model | 1 | 548.092 | 548.092 | 259.835 | 0 |
| Residuals | 142 | 299.533 | 2.109 | ||
| Total | 143 | 847.625 |
The p-value is very small (≈0), so we reject H0.
The data provide strong evidence that population slope, β1, is different from 0.
The data provide sufficient evidence that there is a linear relationship between a cat's heart weight and body weight.
Recap
Recap
- Used analysis of variance to partition variability in the response variable
Recap
Used analysis of variance to partition variability in the response variable
Defined and calculated R2
Recap
Used analysis of variance to partition variability in the response variable
Defined and calculated R2
Used ANOVA to test the hypothesis H0:β1=0 vs Ha:β1≠0