Simple Linear Regression

# Simple Linear Regression
## Prediction
### Prof. Maria Tackett

---

## [Click here for PDF of slides](05-slr-prediction.pdf)

---

## Topics

- Predict the response given a value of the predictor variable

- Use intervals to quantify the uncertainty in the predicted values 
   
--

- Define *extrapolation* and why we should avoid it

---

## Cats data

The data set contains the **heart weight** (.term[Hwt]) and **body weight** (.term[Bwt]) for 144 domestic cats.

---

## Cats data

We want to fit a model so we can use a cat's body weight to predict how much its heart weighs.

---

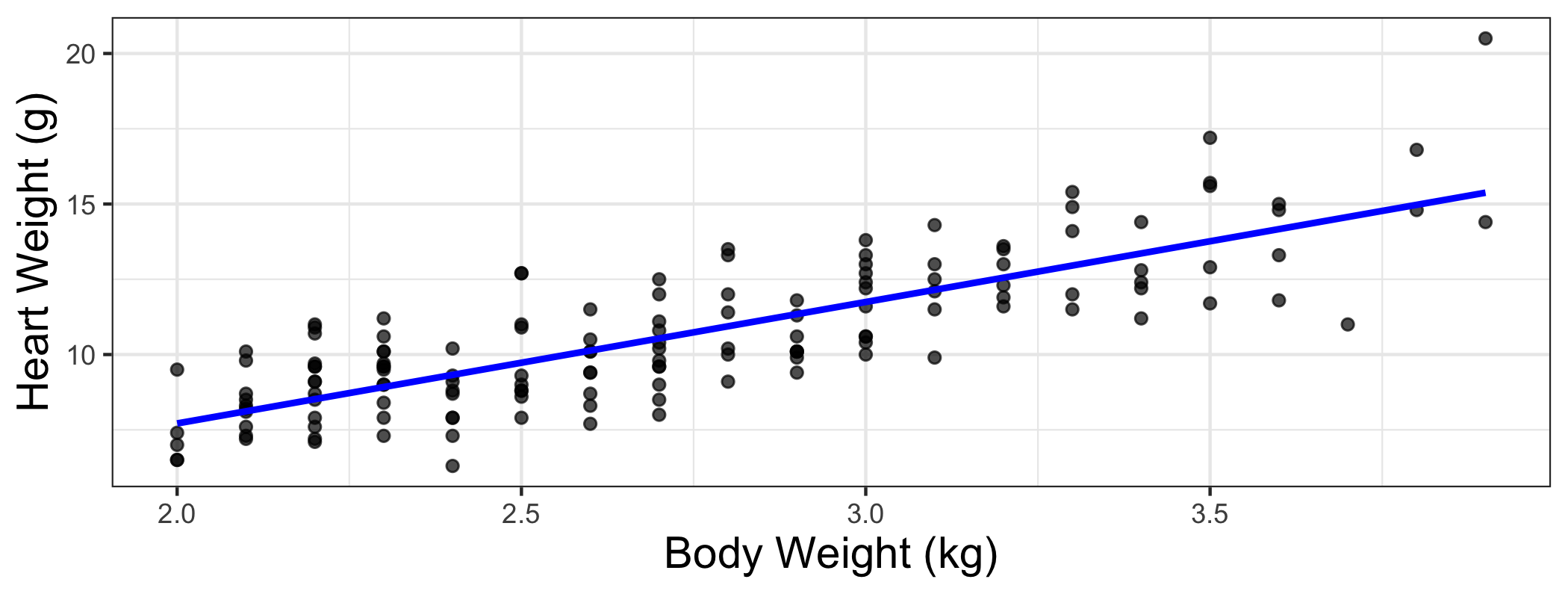
## The model

<br>

<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -0.357 </td>
   <td style="text-align:right;"> 0.692 </td>
   <td style="text-align:right;"> -0.515 </td>
   <td style="text-align:right;"> 0.607 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Bwt </td>
   <td style="text-align:right;"> 4.034 </td>
   <td style="text-align:right;"> 0.250 </td>
   <td style="text-align:right;"> 16.119 </td>
   <td style="text-align:right;"> 0.000 </td>
  </tr>
</tbody>
</table>

---

## Prediction

We can use the regression model to

Estimate the .vocab[<u>mean</u>] response when the predictor variable is equal to a value `$x_0$`

<br>

Predict the response for an .vocab[<u>individual</u>] observation with a value of the predictor equal to `$x_0$`

---

## Calculating a predicted value

Based on this model, about how much does her heart weigh?
]

.pull-right[
<img src="img/05/mindy.JPG" width="60%" height="70%" style="display: block; margin: auto;" />
]

.alert[
$$
`\begin{align}
\hat{\text{Hwt}} &= -0.357 + 4.034 \times \color{purple}{\mathbf{3.18}} \\
&= \mathbf{12.471} \text{ g}
\end{align}`
$$
]

---

## Uncertainty in predictions

.eq[
**Confidence interval for the mean response**
`$$\hat{y} \pm t_{n-2}^* \times \color{purple}{\mathbf{SE}_{\hat{\boldsymbol{\mu}}}}$$`
]

.eq[
**Prediction interval for an individual observation**
`$$\hat{y} \pm t_{n-2}^* \times \color{purple}{\mathbf{SE_{\hat{y}}}}$$`
]

---

## Standard errors

.eq[
`$$SE_{\hat{\mu}} = \hat{\sigma}_\epsilon\sqrt{\frac{1}{n} + \frac{(x-\bar{x})^2}{\sum\limits_{i=1}^n(x_i - \bar{x})^2}}$$`
]

.eq[
`$$SE_{\hat{y}} = \hat{\sigma}_\epsilon\sqrt{1 + \frac{1}{n} + \frac{(x-\bar{x})^2}{\sum\limits_{i=1}^n(x_i - \bar{x})^2}}$$`
]

---

## Standard errors

.eq[
`$$SE_{\hat{\mu}} = \hat{\sigma}_\epsilon\sqrt{\frac{1}{n} + \frac{(x-\bar{x})^2}{\sum\limits_{i=1}^n(x_i - \bar{x})^2}}$$`
]

.eq[
`$$SE_{\hat{y}} = \hat{\sigma}_\epsilon\sqrt{\mathbf{\color{purple}{\Large{1}}} + \frac{1}{n} + \frac{(x-\bar{x})^2}{\sum\limits_{i=1}^n(x_i - \bar{x})^2}}$$`
]

---

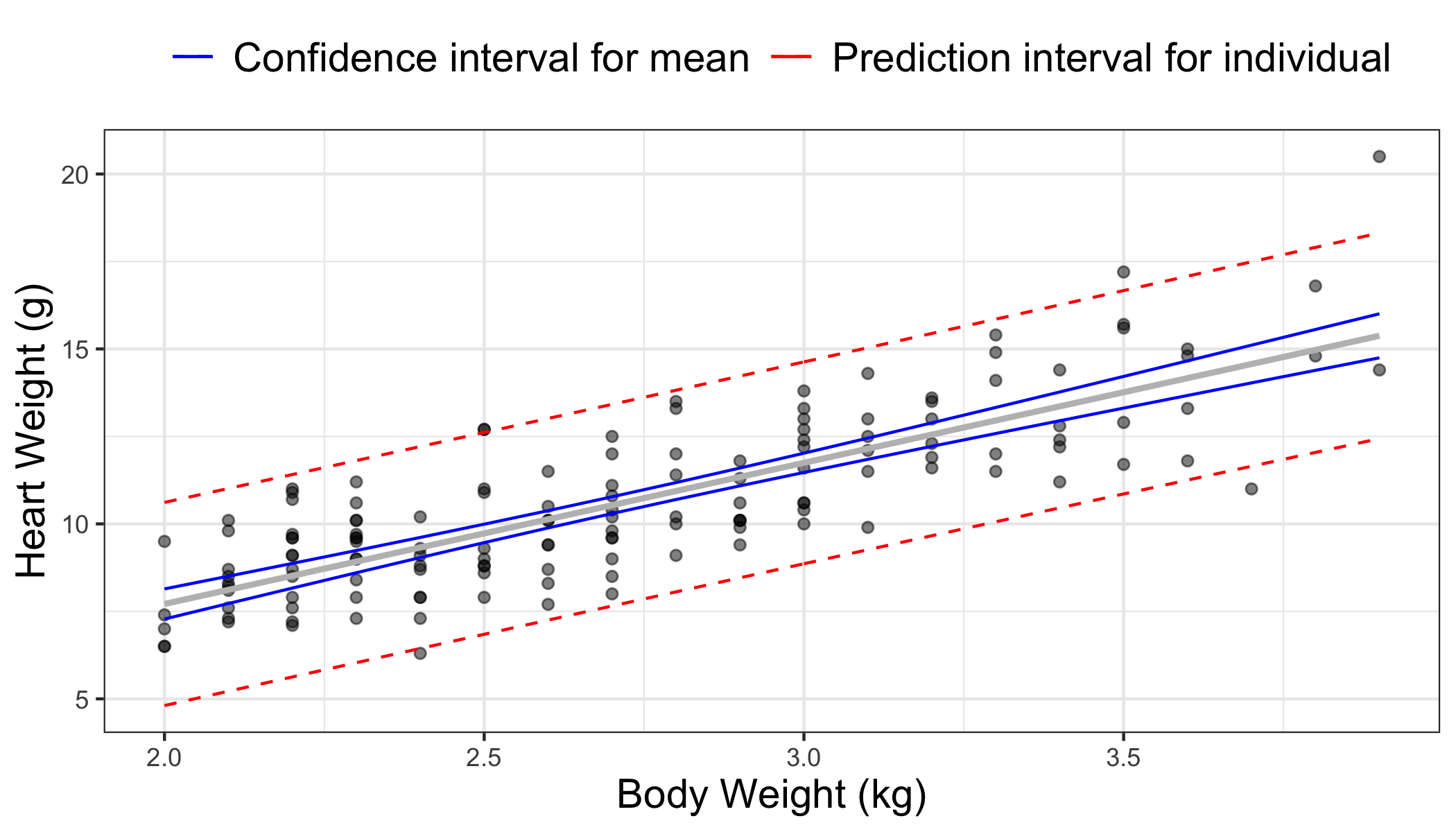
## Confidence interval

The 95% .vocab[confidence interval] for the .vocab[*mean*] heart weight of cats that weigh 3.18 kg is

.alert[
We are 95% confident that mean heart weight for the subset of cats that weigh 3.18 kg is between 12.143 g and 12.801 g.
]
---

## Prediction interval

The 95% .vocab[prediction interval] for an .vocab[*individual*] cat (Mindy) that weighs 3.18 kg is

---

## Comparing intervals

---

## 🛑 Caution! Extrapolation

We should **<u>not</u>** use the model to predict for values of `$X$` far outside the range of values used to fit the model.

<br>

This is called .vocab[extrapolation]. 
---

## Predict Andy's heart weight?

<br>

Should we use this regression model to predict how much his heart weighs?
]

.pull-right[
<img src="img/05/andy.JPG" width="75%" height="85%" style="display: block; margin: auto;" />
]

---

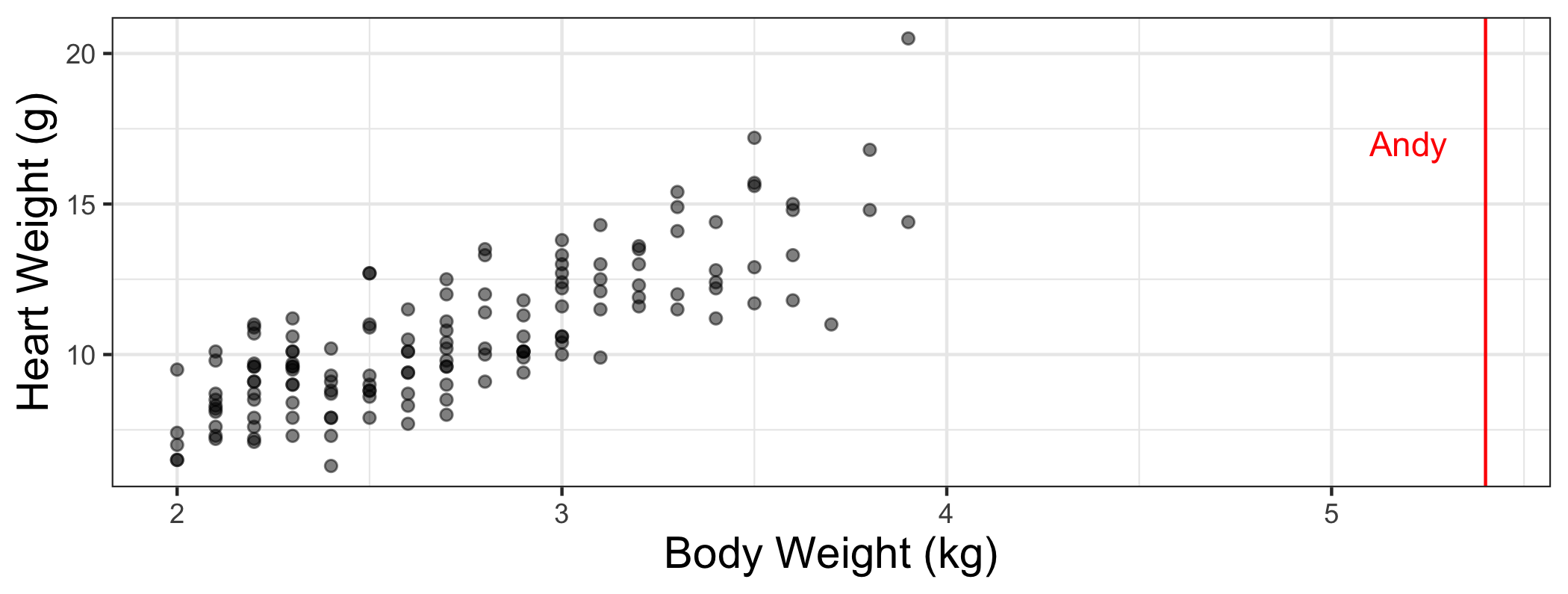
## Predict Andy's heart weight?

We should **<u>not</u>** use this model to predict Andy's heart weight, since that would be .vocab[extrapolation].

---

## Recap

- Predicted the response given a value of the predictor variable

- Used intervals to quantify the uncertainty in the predicted values 
    - Confidence interval for the mean response
    - Prediction interval for individual response

- Defined .vocab[extrapolation] and why we should avoid it