Simple Linear Regression
Foundation
Prof. Maria Tackett
1
General form of model
Y=f(X)+ϵ
3
General form of model
Y=f(X)+ϵ
Y: response variable
3
General form of model
Y=f(X)+ϵ
Y: response variable
X: predictor variable
3
General form of model
Y=f(X)+ϵ
Y: response variable
X: predictor variable
f: fixed but unknown function
3
General form of model
Y=f(X)+ϵ
Y: response variable
X: predictor variable
f: fixed but unknown function
ϵ: random error
3
Simple linear regression
4
Simple linear regression
Y=Model+Error=f(X)+ϵ=μY|X+ϵ=β0+β1X+ϵ
4
Y=β0+β1X+ϵ
where the errors are independent and normally distributed ϵ∼N(0,σ2ϵ)
5
Y|X∼N(β0+β1X,σ2ϵ)
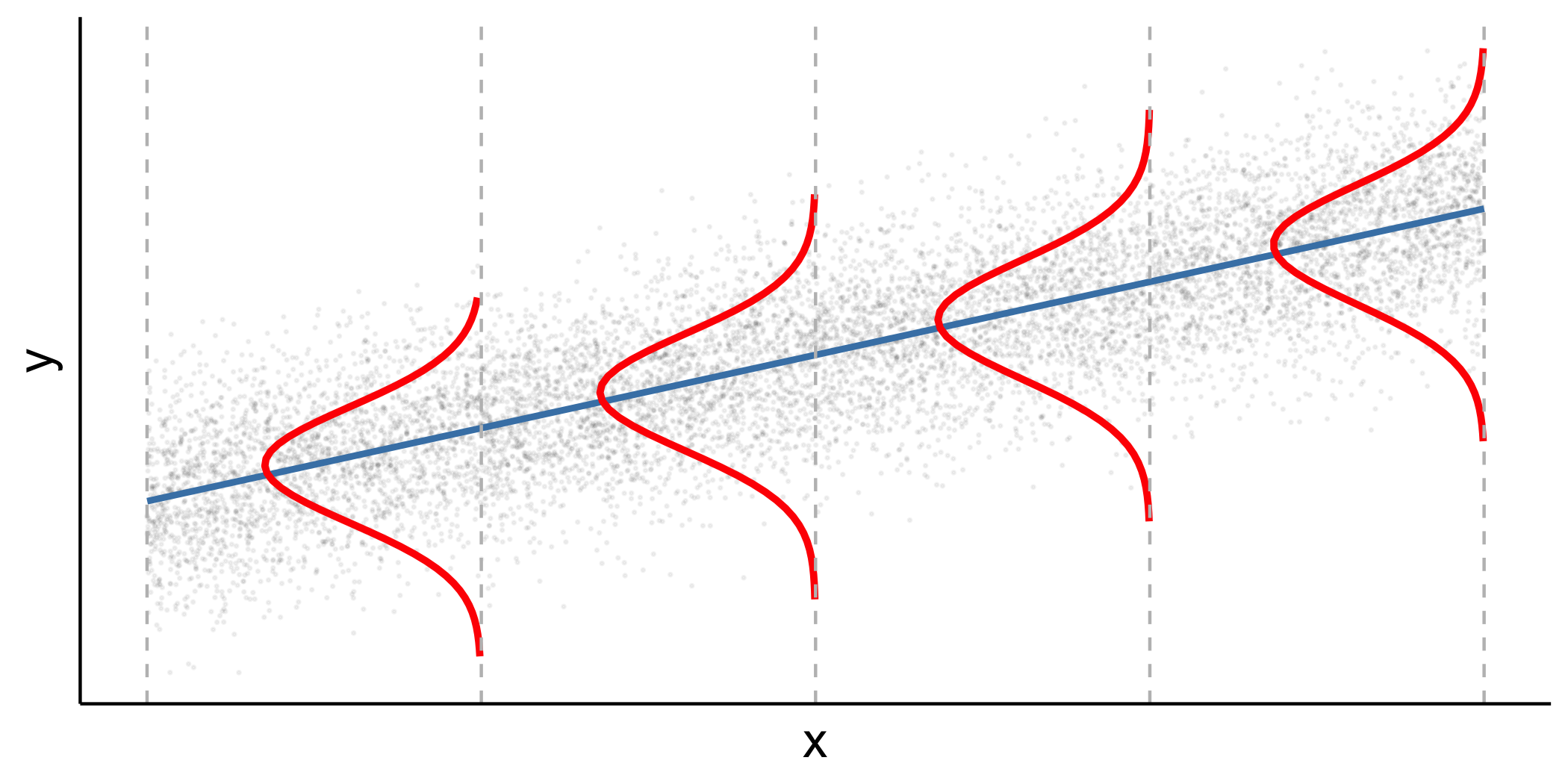
6
Y|X∼N(β0+β1X,σ2ϵ)
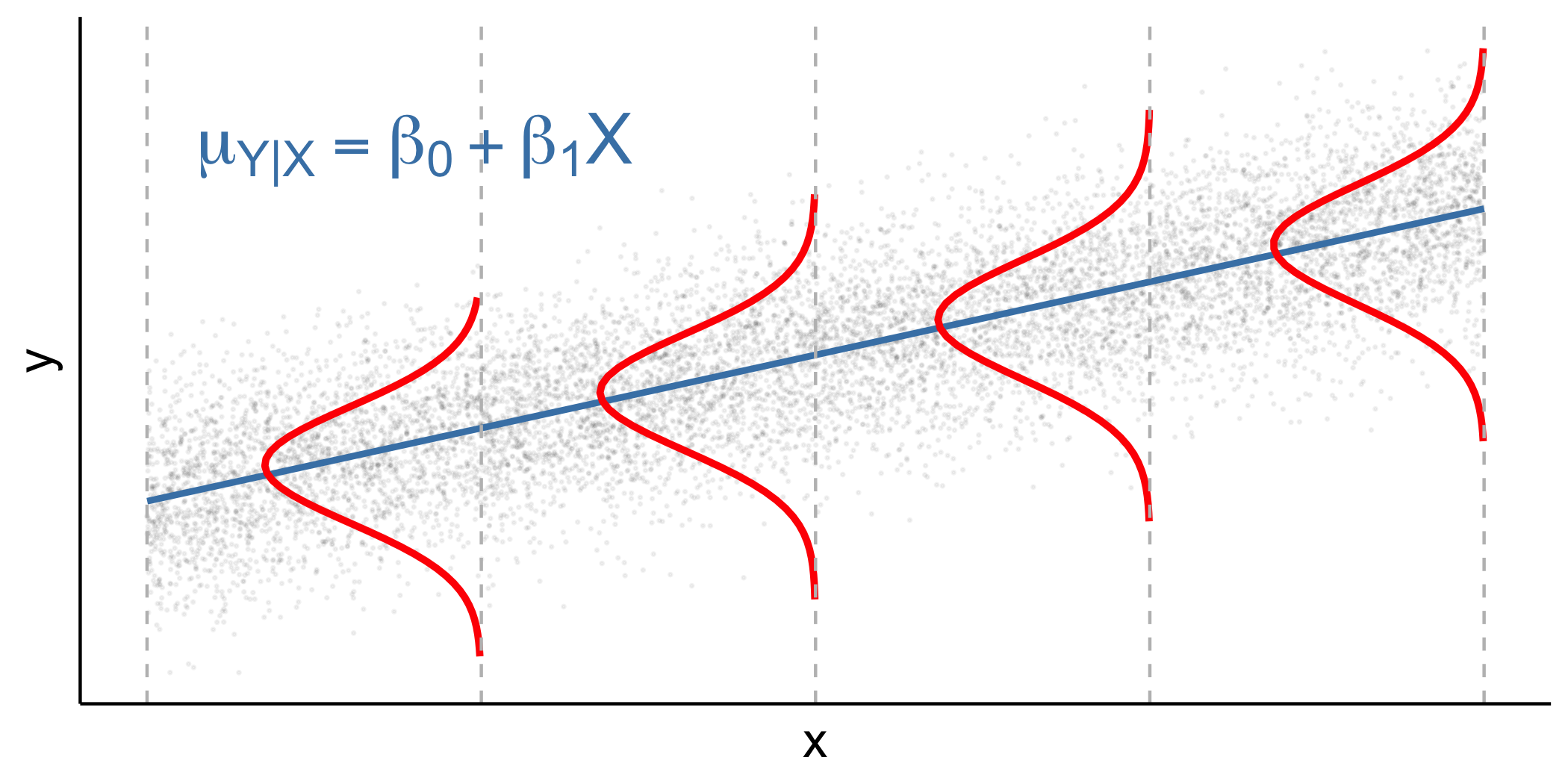
7
Y|X∼N(β0+β1X,σ2ϵ)
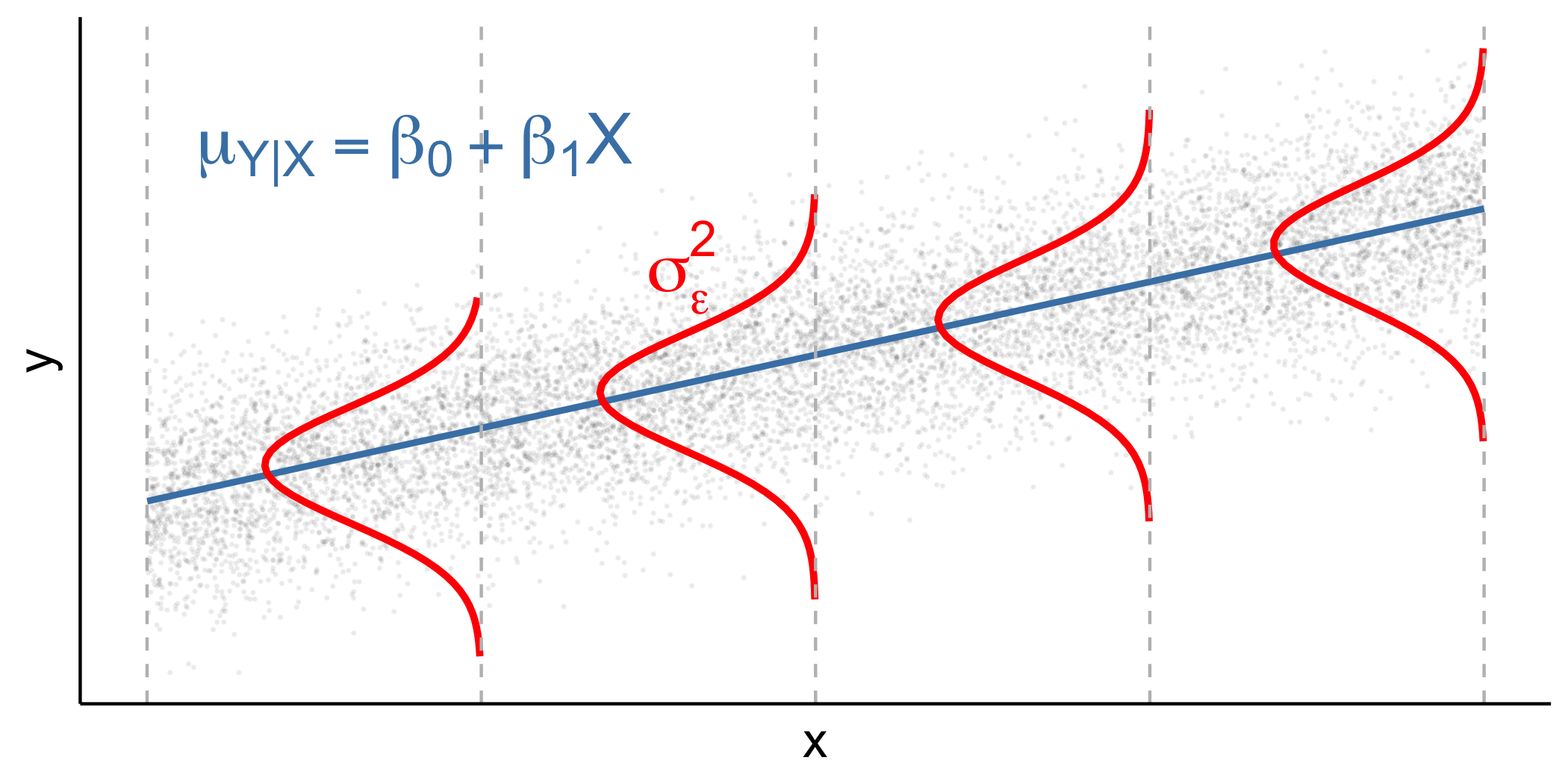
8
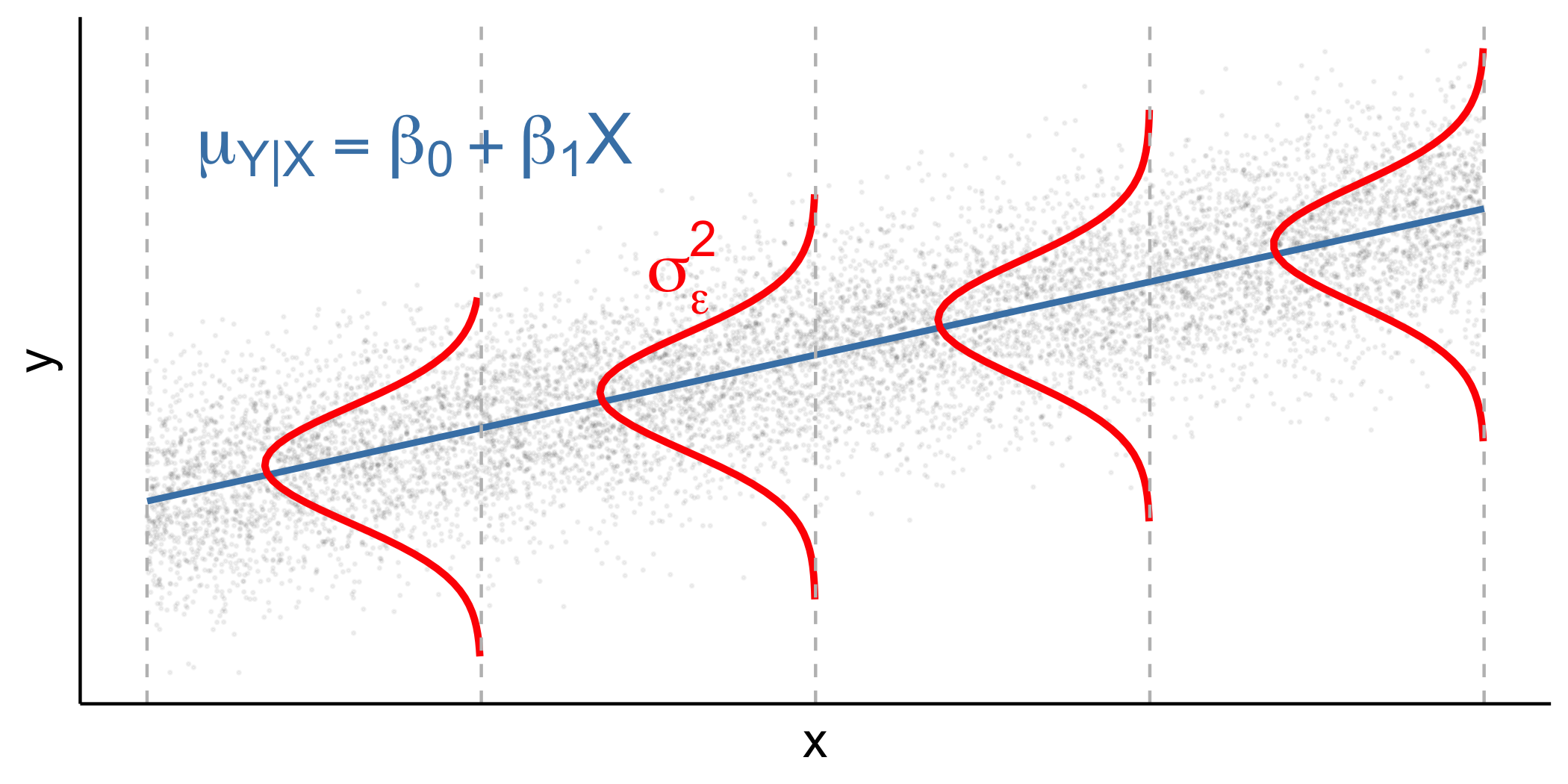
Regression standard error
Once we fit the model, we can use the residuals to calculate the regression standard error
ˆσϵ=√n∑i=1(yi−ˆyi)2n−2=√n∑i=1e2in−2
9
Standard error of ˆβ1
SEˆβ1=ˆσϵ√1(n−1)s2X
10
11