Simple Linear Regression
Introduction
Prof. Maria Tackett
Topics
- Use simple linear regression to describe the relationship between a quantitative predictor and quantitative response variable.
Topics
Use simple linear regression to describe the relationship between a quantitative predictor and quantitative response variable.
Estimate the slope and intercept of the regression line using the least squares method.
Topics
Use simple linear regression to describe the relationship between a quantitative predictor and quantitative response variable.
Estimate the slope and intercept of the regression line using the least squares method.
Interpret the slope and intercept of the regression line.
Movie ratings data
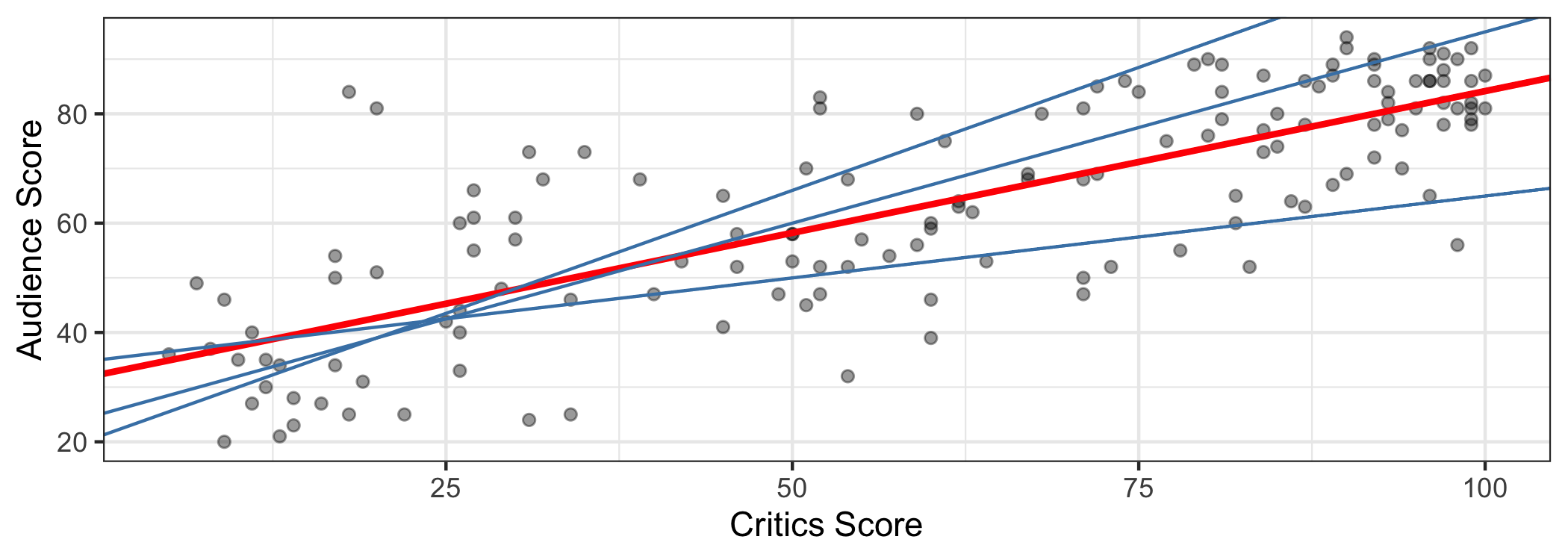
The data set contains the "Tomatometer" score (critics) and audience score (audience) for 146 movies rated on rottentomatoes.com.
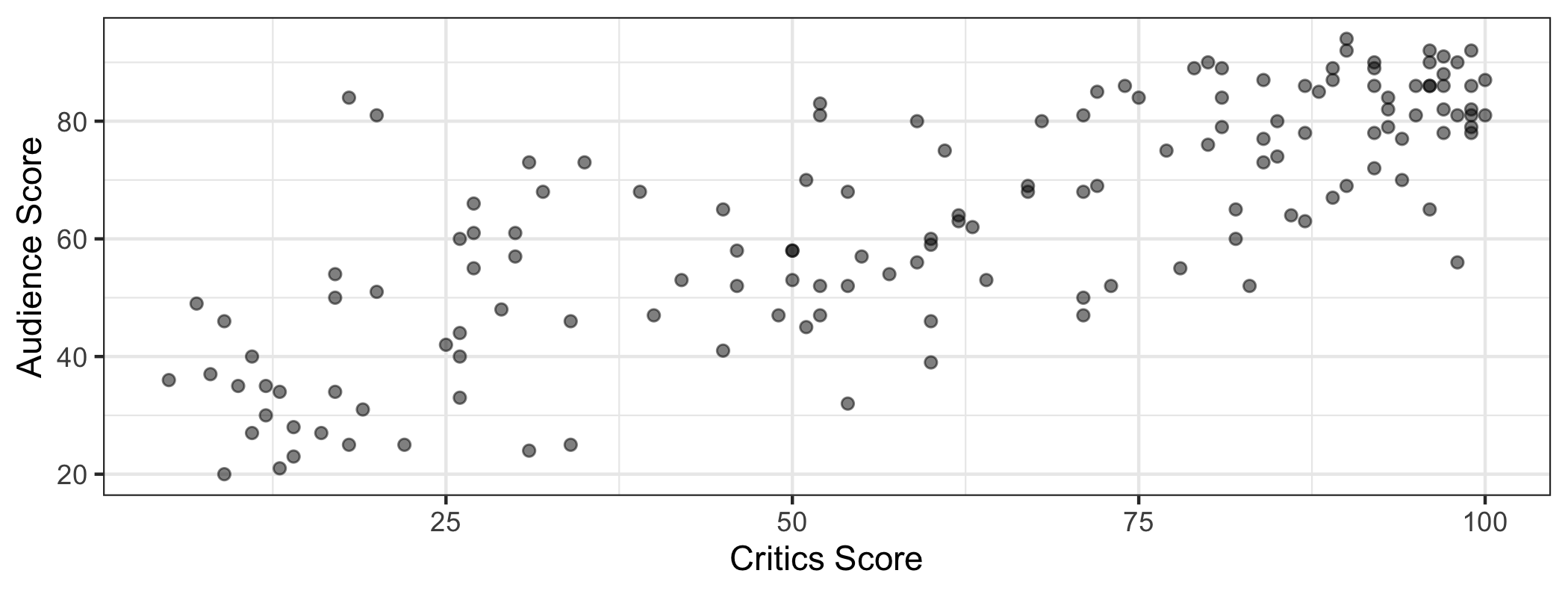
Movie ratings data
We want to fit a line to describe the relationship between the critics score and audience score.
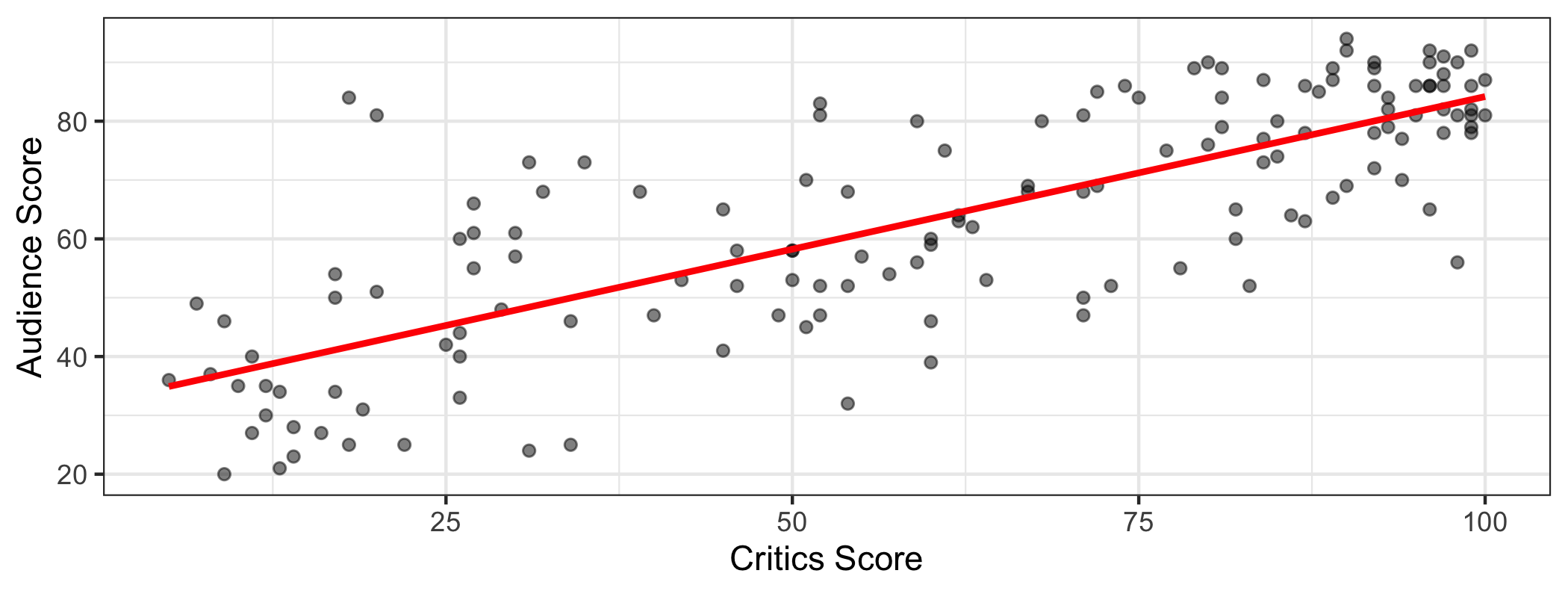
Terminology
The response, Y, is the variable describing the outcome of interest.
The predictor, X, is the variable we use to help understand the variability in the response.
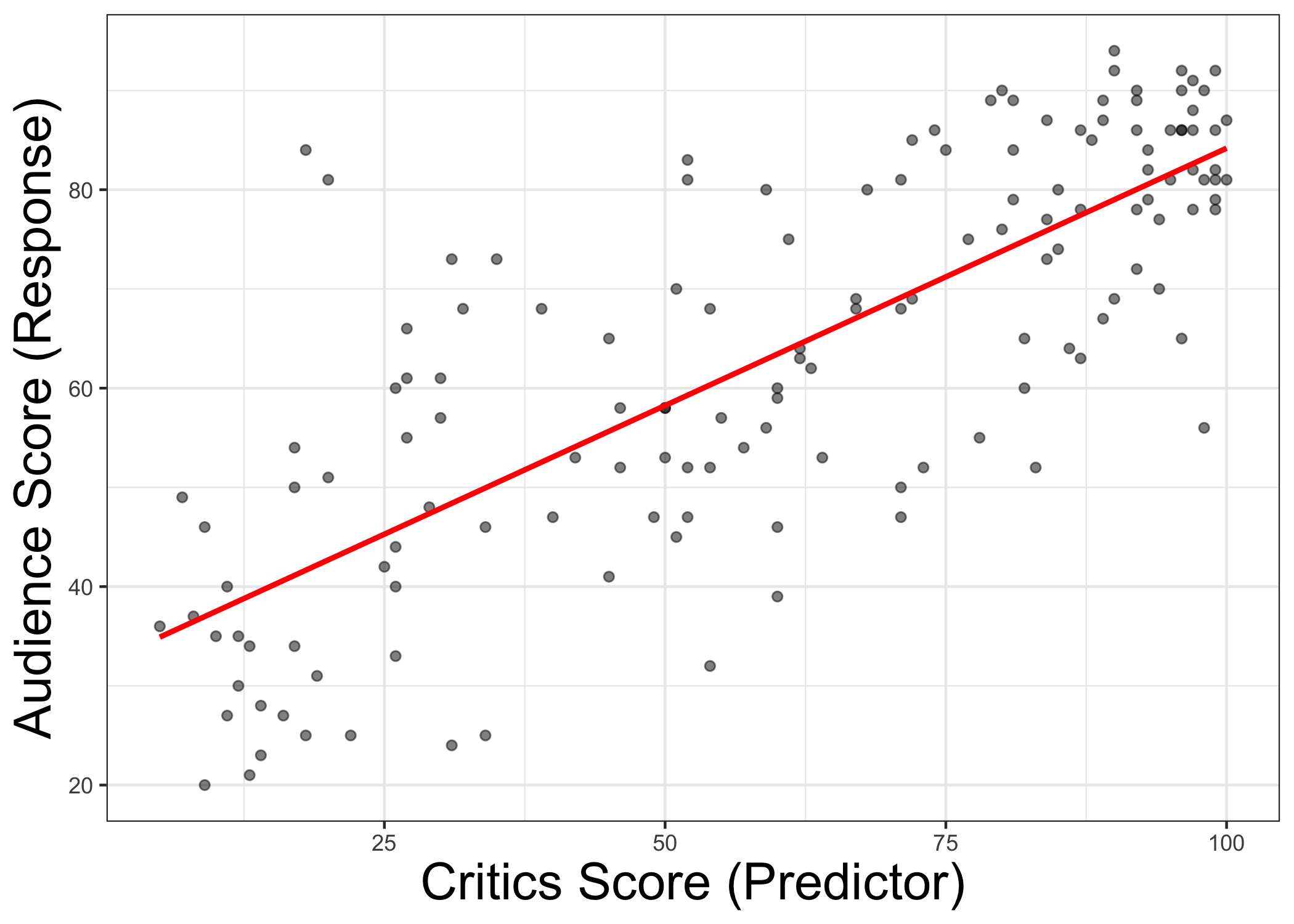
Regression model
A regression model is a function that describes the relationship between the response, Y, and the predictor, X.
Y=Model+Error=f(X)+ϵ=μY|X+ϵ
Y=Model+Error=f(X)+ϵ=μY|X+ϵ
Y=Model+Error=f(X)+ϵ=μY|X+ϵ
Simple linear regression
When we have a quantitative response, Y, and a single quantitative predictor, X, we can use a simple linear regression model to describe the relationship between Y and X.
Y=β0+β1X+ϵ
β1:Slopeβ0:Intercept
ˆY=ˆβ0+ˆβ1X
ˆY=ˆβ0+ˆβ1X
How do we choose values for ˆβ1 and ˆβ0?
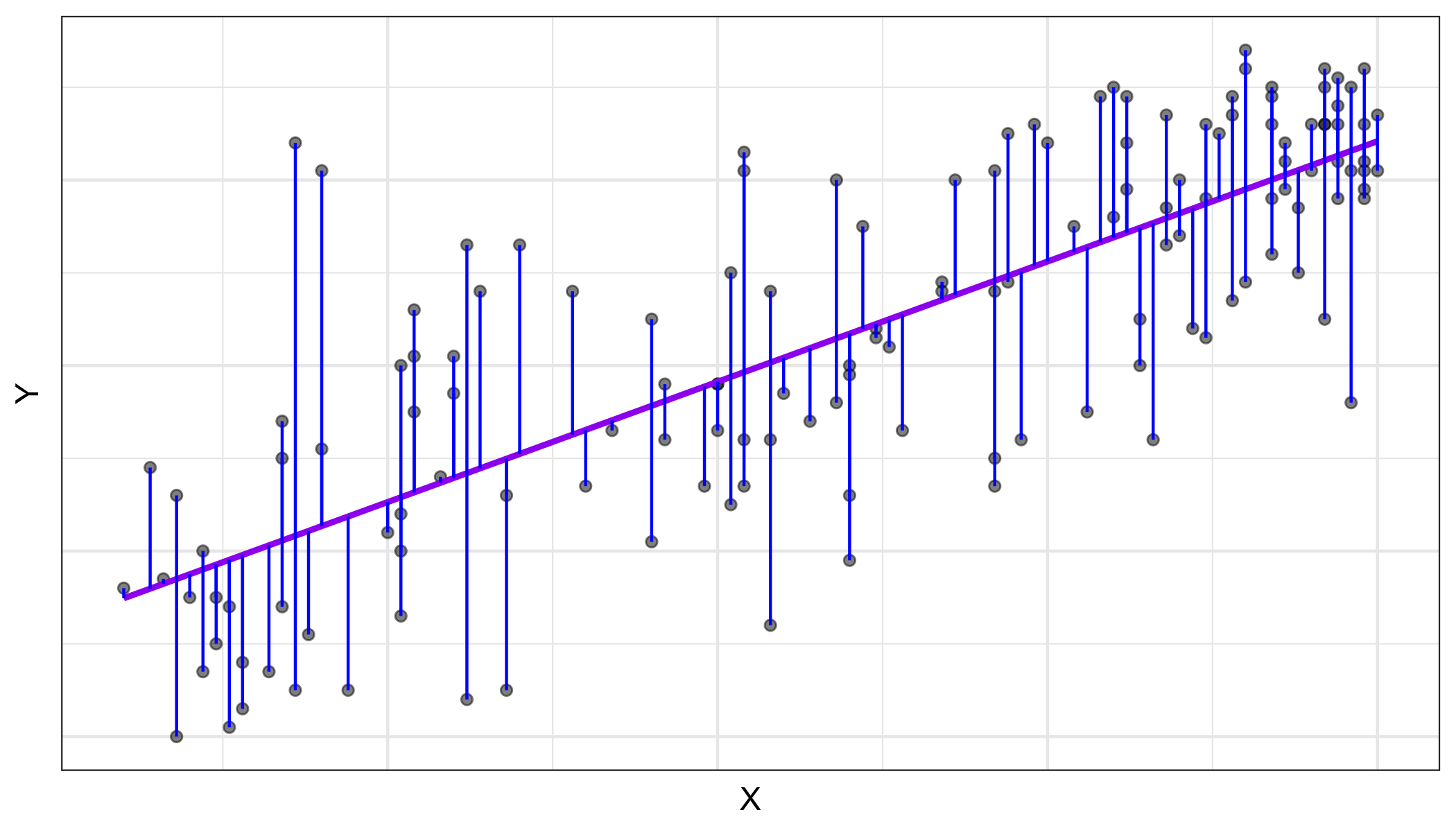
Residuals
residual=observed−predicted=y−ˆy
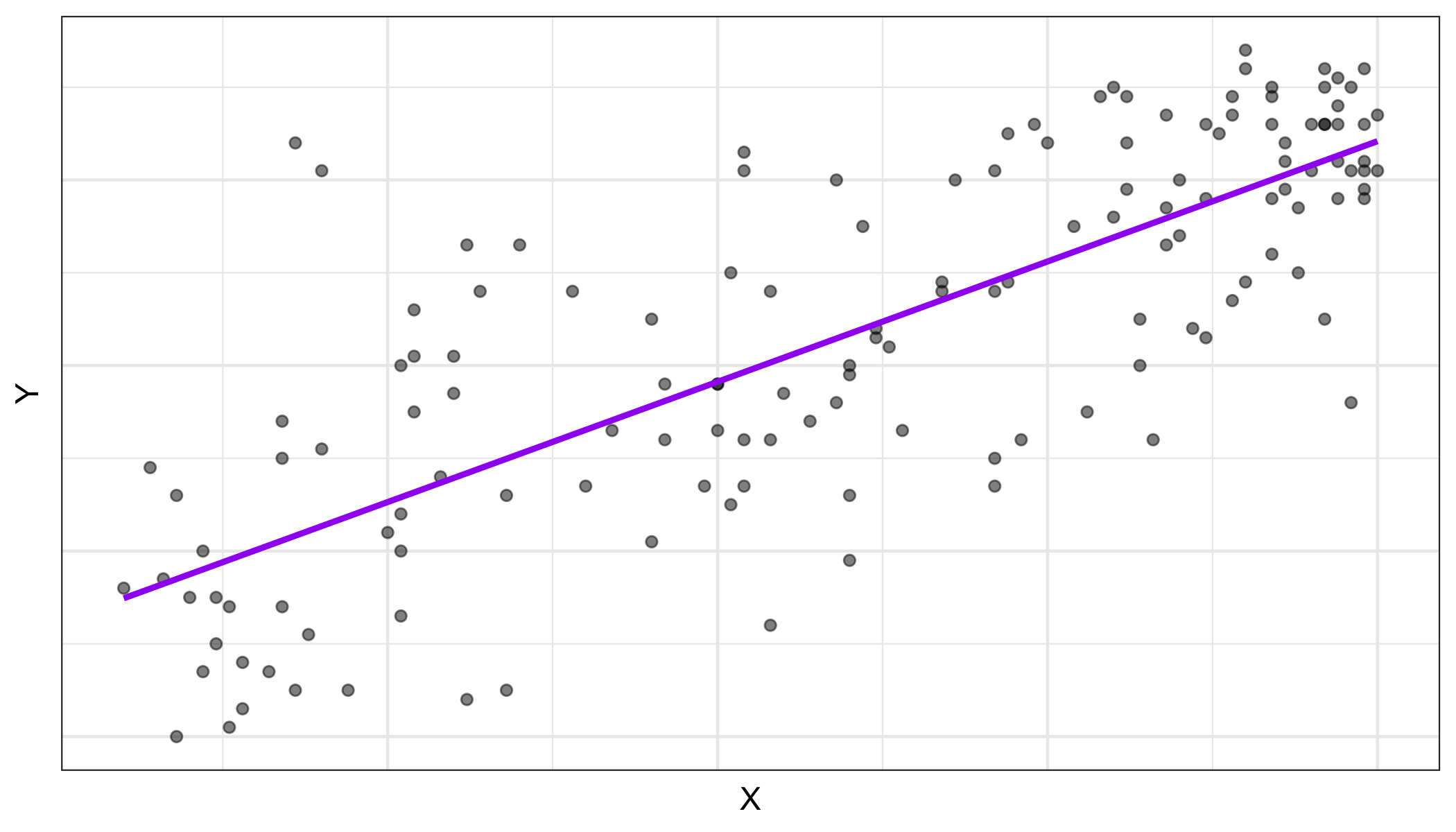
Least squares line
Least squares line
- The residual for the ith observation is
ei=observed−predicted=yi−ˆyi
Least squares line
- The residual for the ith observation is
ei=observed−predicted=yi−ˆyi
- The sum of squared residuals is
e21+e22+⋯+e2n
Least squares line
- The residual for the ith observation is
ei=observed−predicted=yi−ˆyi
- The sum of squared residuals is
e21+e22+⋯+e2n
- The least squares line is the one that minimizes the sum of squared residuals
Estimating the slope
ˆβ1=rsYsX
Estimating the slope
ˆβ1=rsYsX
sX=30.169sY=20.024r=0.781
Estimating the slope
ˆβ1=rsYsX
sX=30.169sY=20.024r=0.781
ˆβ1=0.781×20.02430.169=0.518
Estimating the intercept
ˆβ0=ˉY−ˆβ1ˉX
Estimating the intercept
ˆβ0=ˉY−ˆβ1ˉX
ˉx=60.850ˉy=63.877ˆβ1=0.518
Estimating the intercept
ˆβ0=ˉY−ˆβ1ˉX
ˉx=60.850ˉy=63.877ˆβ1=0.518
ˆβ0=63.877−0.518×60.850=32.296
Interpreting slope & intercept
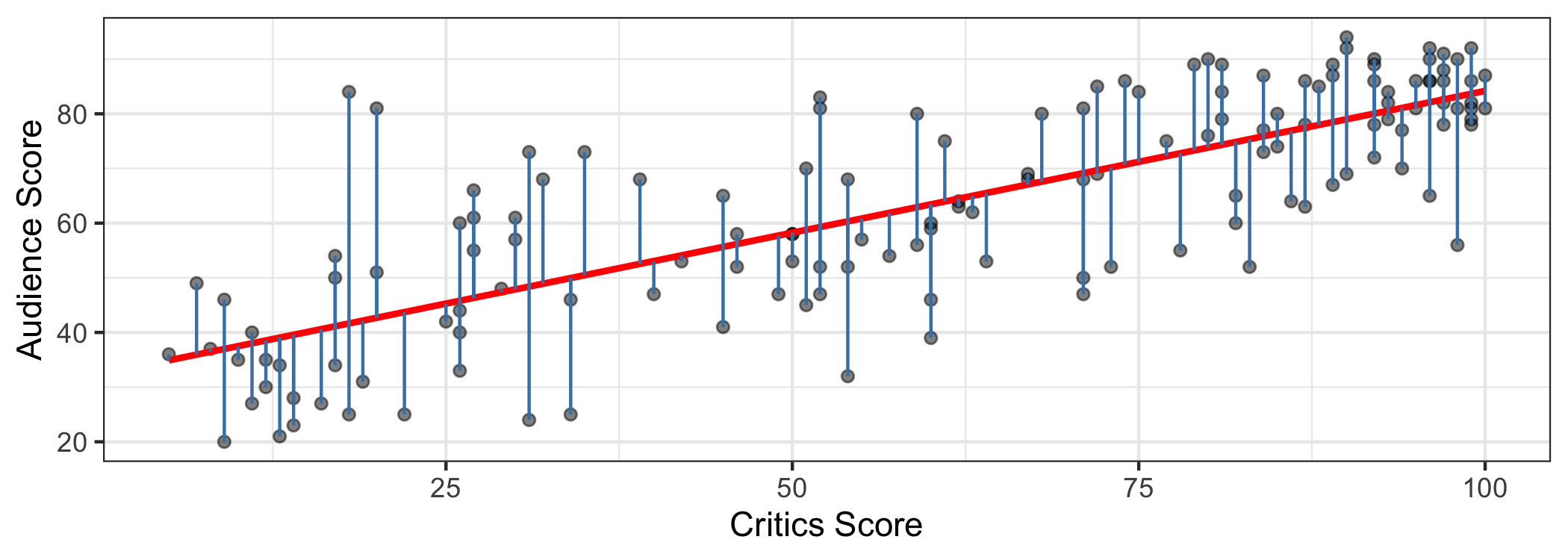
^audience=32.296+0.518×critics
Interpreting slope & intercept
^audience=32.296+0.518×critics
Slope: For every one point increase in the critics score, we expect the audience score to increase by 0.518 points, on average.
Interpreting slope & intercept
^audience=32.296+0.518×critics
Slope: For every one point increase in the critics score, we expect the audience score to increase by 0.518 points, on average.
Intercept: If the critics score is 0 points, we expect the audience score to be 32.296 points.
Does it make sense to interpret the intercept?
Does it make sense to interpret the intercept?
✅ Interpret the intercept if
- the predictor can feasibly take values equal to or near zero.
- there are values near zero in the data.
Does it make sense to interpret the intercept?
✅ Interpret the intercept if
- the predictor can feasibly take values equal to or near zero.
- there are values near zero in the data.
🛑 Otherwise, don't interpret the intercept!
Recap
Recap
- Used simple linear regression to describe the relationship between a quantitative predictor and quantitative response variable.
Recap
Used simple linear regression to describe the relationship between a quantitative predictor and quantitative response variable.
Used the least squares method to estimate the slope and intercept.
Recap
Used simple linear regression to describe the relationship between a quantitative predictor and quantitative response variable.
Used the least squares method to estimate the slope and intercept.
- We interpreted the slope and intercept.
- Slope: For every one unit increase in x, we expect y to change by ˆβ1 units, on average.
- Intercept: If x is 0, then we expect y to be ˆβ0 units.